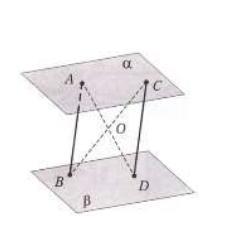
Плоскости α и β параллельны, прямые AB и CD
также параллельны. Площадь треугольника
BOD равна 5. Найдите площадь
четырехугольника ABCD

Через две параллельные проходит единственная плоскость, ABD.

Если две параллельные плоскости (a || b) пересечены третьей (ABD), то линии пересечения параллельны, AC || BD.

ABDC - параллелограмм.

Диагонали параллелограмма точкой пересечения делятся пополам.

Тогда отрезки AO, BO, CO, DO - медианы в соответствующих треугольниках.

Медиана делит площадь треугольника пополам.

Таким образом S(AOB)=S(BOD)=S(COD)=S(AOC)

S(ABDC) =4 S(BOD) =5*4 =20