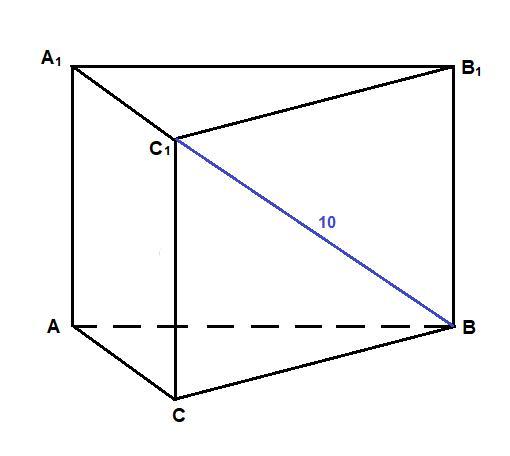
У правильній трикутній призмі діагональ бічної грані дорівнює 10
см. Обчислити бічну поверхню призми, якщо радіус кола,
описаного навколо основи дорівнює 2√3 см.

Ответ:

144 см²

Объяснение:

Основание правильной треугольной призмы - правильный треугольник.

Радиус окружности, описанной около правильного треугольника, вычисляется по формуле:

где а - сторона треугольника.

а = 6 см - ребро основания.

ΔСС₁В: ∠С₁СВ = 90°, по теореме Пифагора

 СС₁ = √(ВС₁² - ВС²) = √(10² - 6²) = √(100 - 36) = √64 = 8 см

Площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра:

S = (6 · 3) · 8 = 144 см²