Предмет: Алгебра,
автор: kmezenceva931
Помогите пожалуйста((
Приложения:
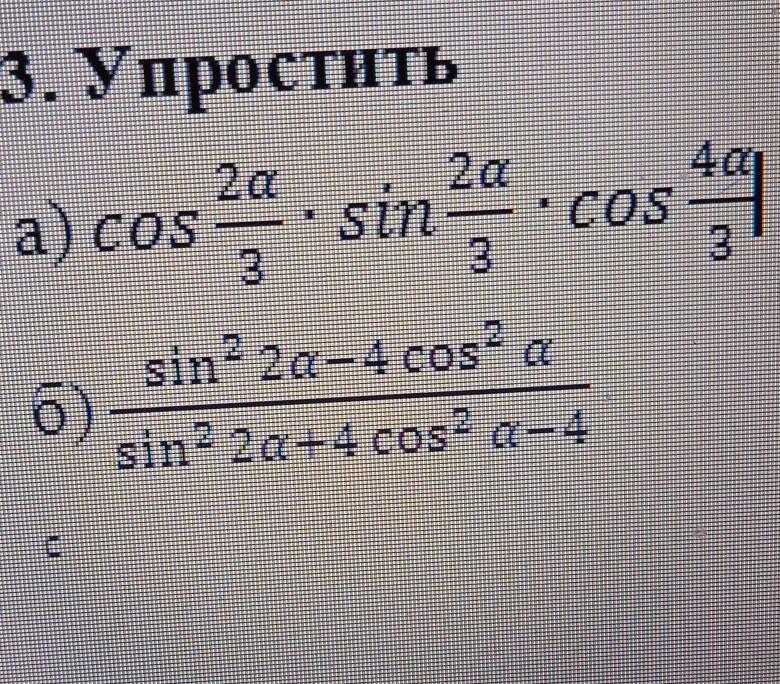
slava13213:
Под б : верхняя дробь cot2(α)(sin(α)+1)(sin(α)−1) нижняя дробь (cos(α)+1)(cos(α)−1)
Ответы
Автор ответа:
1
спасибо большое!!
Интересные вопросы
Предмет: Русский язык,
автор: UniicornNii
Предмет: Русский язык,
автор: СуперГероиня11
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: ghostdz