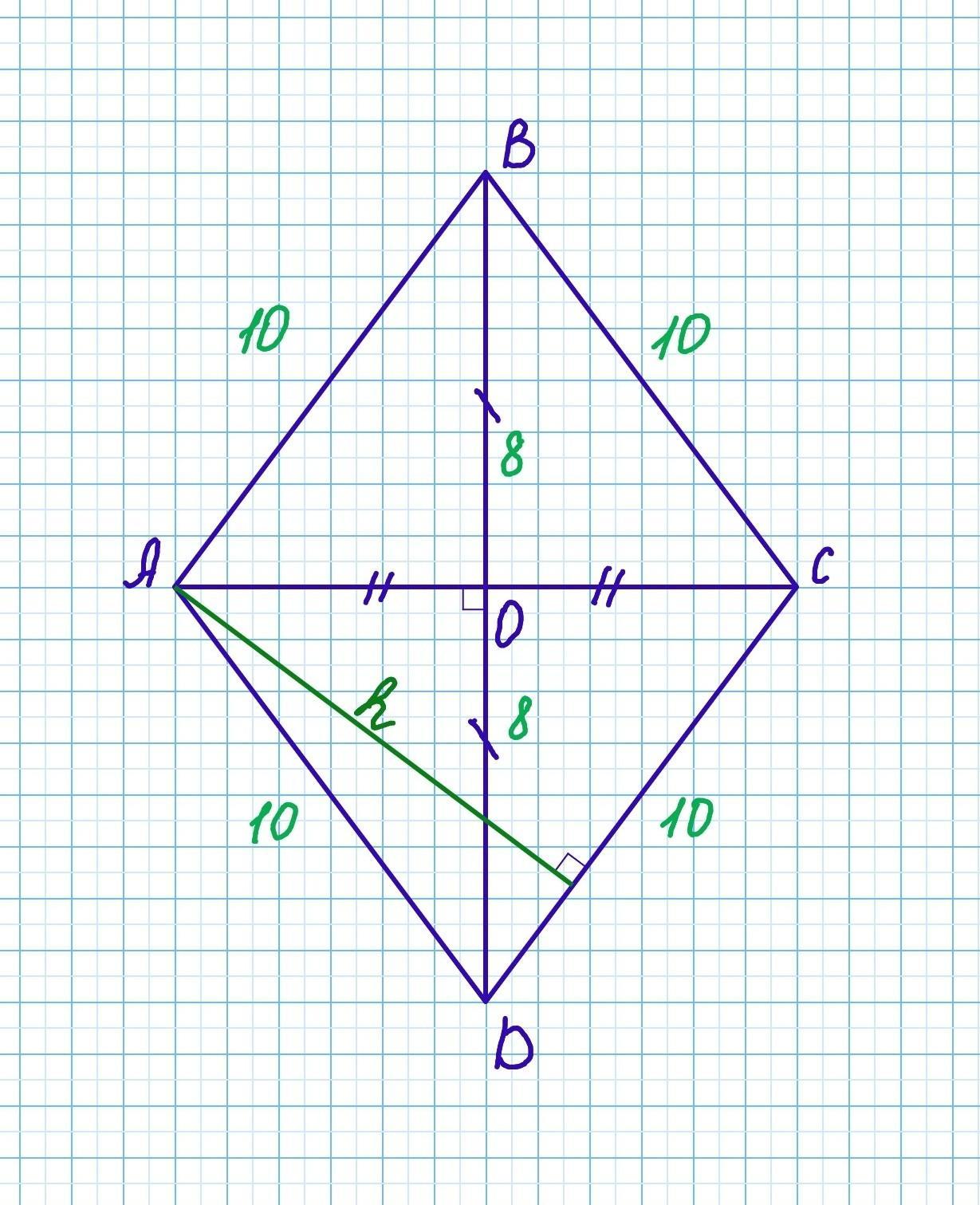
Сторона ромба дорівнює 10 см, а одна з діагоналей - 16 см.
1) Знайдіть площу ромба.
1) Знайдіть висоту ромба.

Ответ: Площадь ромба 96 см²,

висота ромба 9,6 см

Объяснение:

Дано: ABCD - ромб. АВ=10 см, BD=16см.

Знайти: а) S(ABCD)

б) h -?

• Ромбом називається паралелограм, у якого всі сторони рівні:

АВ=BC=CD=AD=10см

• Діагоналі ромба точкою перетину діляться навпіл:

BO=OD=16:2=8 см

• Діагоналі ромба взаємно перпендикулярні:

BD⟂AC

РІШЕННЯ

Розглянемо прямокутний трикутник АОВ, та знайдемо катет ОА за теоремою Піфагора:

ОА²=АВ²-ВО²=10²-8²=100-64=36

ОА=√36=6см

a) Знайдемо площу ромба

І спосіб

• Діагоналі ділять ромб на чотири рівні прямокутні трикутники.

Знайдемо площу прямокутного трикутника АОВ.

• Площа прямокутного трикутника дорівнює половині добутку його катетів.

см².

Тоді площа ромба:

см².

ІІ спосіб.

• Площа ромба рівна половині добутку діагоналей:

АС=2×ОА=2×6=12см

см²

б) Знайдемо висоту ромба.

Площу ромба також можна знайти за формулою:

S=ah,

a - сторона ромба, h - його висота.

Тоді:

см

#SPJ1