Предмет: Алгебра, автор: zxcuser22

Найдите промежутки возрастания функции (Она на фото!!!!)

Приложения:

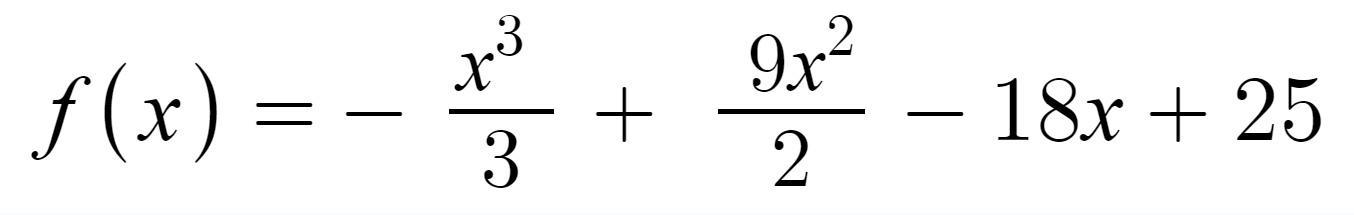
Ответы

Автор ответа: Fire1ce

2

Найти промежутки возрастания функции f(x)=(-x³/3)+9x²/2-18x+25.

Ответ:

Функция возрастает при х ∈ [3;6].

Объяснение:

Найдём производную функции:

$\Large \boldsymbol {} f'(x)=(-\frac{x^3}{3} +\frac{9x^2}{2} -18x+25)'=(-\frac{1}{3}x^3)'+(\frac{9}{2}x^2)'-\\\\ -(18x)'+(25)'=-\frac{1}{3}*3x^{3-1} +\frac{9}{2} *2x^{2-1} -18*1=\\\\=-x^2+9x-18$

Найдём критические точки.

$\Large \boldsymbol {} -x^2+9x-18=0 \\\\x\in(-\infty;+\infty)\\\\D=b^2-4ac=9^2-4*(-1)*(-18)=9\\\\x_1=\frac{-b+\sqrt{D} }{2a}=\frac{-9+\sqrt{9} }{-2*1} =\frac{-9+3}{-2}=3\\\\ x_1=\frac{-b-\sqrt{D} }{2a}=\frac{-9-\sqrt{9} }{-2*1} =\frac{-9-3}{-2}=6$

Разбиваем крит. точками координатную плоскость на промежутки:

$\Large \boldsymbol {} ----\boxed{3}++++\boxed{6} ----$

Функция возрастает на промежутках, где её производная больше нуля, убывает - меньше нуля.

Функция возрастает при х ∈ [3;6].

Функция убывает при х ∈ (-∞;3]U[6;+∞).

zxcuser22: Мужик - ты гений. Спасибо за помощь)

Fire1ce: не за что))

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: miroslava2010

Прочитай отрывок из песенки Винни-Пуха, который только что съел мёд из горшка. Найди в нём имена существительные. Что ты знаешь о каждом из них? Напиши по образцу: Горшок - (что?), н.ф.(что?) горшок - сущ., неодуш.,м.р., ед.ч. Разочарования - (что?), н.ф.(что?) разочарование - сущ., неодущ., ср.р., мн.ч.

2 года назад

Предмет: Русский язык, автор: UltryYt

Срочно Помогите 4 упр

2 года назад

Предмет: Русский язык, автор: yasminkuzmina

слова с суффиксами еньк(а) ик ок юшк(о) чик(и)оньк(а)

2 года назад

Предмет: Математика, автор: 123456784650

построй ломанную линию помогите как рисоват

8 лет назад

Предмет: Геометрия, автор: luv80

Помогите,пожалуйста решить!!!!!

8 лет назад