Предмет: Геометрия, автор: oleksandravlog3

менша сторона прямокутника дорівнює 3 см, а кут між діагоналями 120⁰ знайдіть більшу сторону прямокутника
Допоможіть будь ласка!

Ответы

Автор ответа: 68tata

Відповідь:

3√3 см

Пояснення:

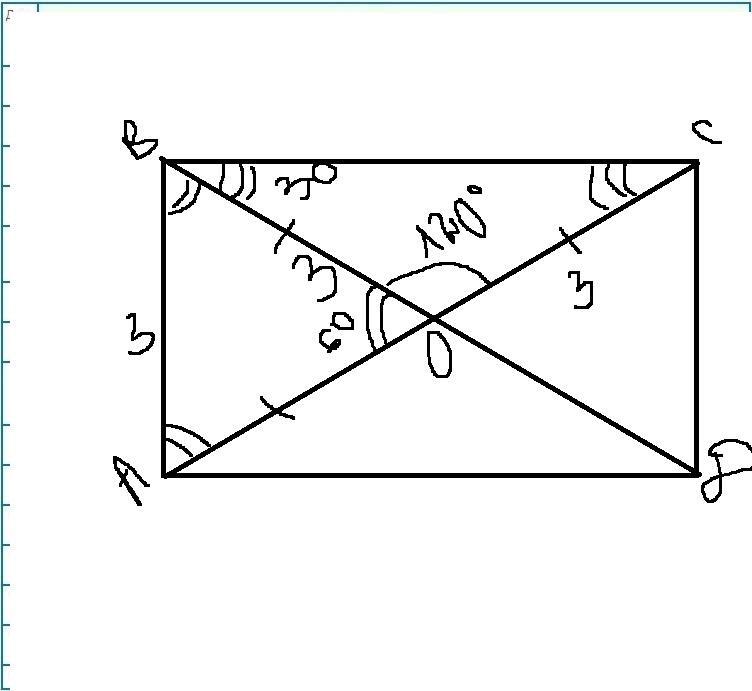
Дано: АВСД- прямокутник,
АВ=3 см, ∠ВОС=120°
Знайти : ВС -?
Рішення:
за допомогою формул площи прямокутника , за допомогою теореми синусів, за допомогою тереми Піфагора
Розглянемо малюнок: ∠АОВта ∠ВОС- суміжні, отже ∠АОВ+∠ВОС=180° → ∠АОВ=180°- ∠ВОС=180°-120°=60°.
За властивістю діагоналей прямокутника вони в точці перетину діляться навпіл , та є рівними, отже АО=ОВ, отже ∠ВАО=∠АВО.За теоремою про суми кутів трикутника ∠ВАО+∠АВО+∠ВОС=180° →
2∠ВАО=180°-60°;
∠ВАО=120°2;
∠ВАО=∠АВО=60°, отже ΔАОВ- правильний та ВА=АО=ОВ=3 см.
АО=ОС, тоді АС=АО+ОС=6см.
1 варіант :Площа прямокутника обчислюється за формулою:
S= 1/2* AC²*sin120°=1/2*6²*√3/2=9√3.
S=AB*BC →BC= S: AB= 19√3:3=3√3
2 варіант через теорему синусів:
( всі обчислення до слів перший варіант записуємо і далі продовжуємо) розглянемо ΔВОС, так як ВО=ОС ( властивість діагоналей прямокутника), то ∠ОВС=∠ОСВ. За теоремою про суми кутів трикутника: ∠ОВС=∠ОСВ=(180°-120°):2=30°.
За теоремою синусів:
$\frac{BO}{sin 30}=\frac{BC}{sin 120};\\ \\ \frac{3}{\frac{1}{2} }=\frac{BC}{\frac{\sqrt{3} }{2} } ;\\ \\\frac{3}{1}=\frac{BC}{\sqrt{3} };\\ BC=3\sqrt{3}$
3 варіант
розглянемо Δ АВС, ∠В=90°, катет АВ=3 см. Гипотинуза АС=АО+ОС=3+3=6см.
За теоремою Піфагора
АС²=АВ²+ВС² →ВС²=АС²-АВ²
$BC=\sqrt{6^2-3^2}=\sqrt{27}=\sqrt{9*3}=3\sqrt{3}$ (cм)