Предмет: Алгебра, автор: Reideen

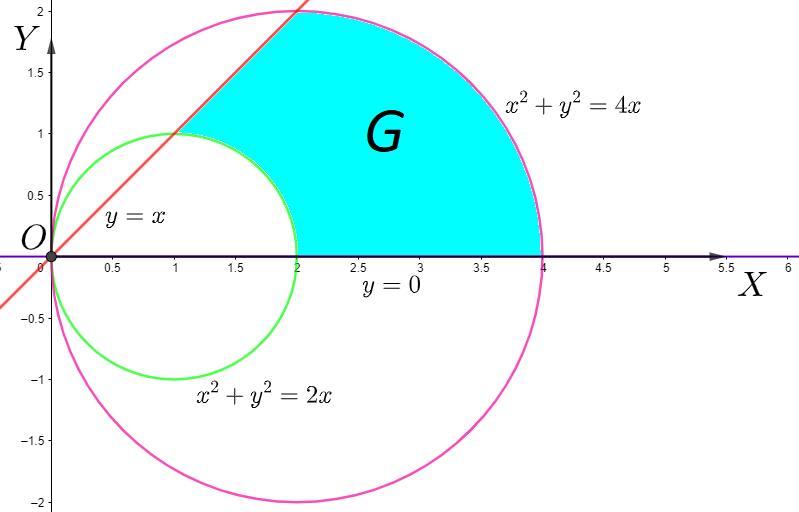
Вычислить с помощью двойного интеграла

Приложения:

Ответы

Автор ответа: mathkot

Ответ:

$\boxed{ \boldsymbol{ S = \dfrac{3\pi + 6}{4}} }$ квадратных единиц

Примечание:

Переход от декартовых координат к полярным в двойном интеграле можно осуществить с помощью якобиана перехода.

(в данном случае переход осуществляются для формулы вычисления площади в декартовой системе координат через двойной интеграл)

$\boxed{ \boldsymbol{ \displaystyle \iint\limits_{G} \, dxdy = \iint\limits_{G} r \, drd\phi = \int\limits^{\beta }_{\alpha } \, d\phi \int\limits^{r_{2}(\phi)}_{r_{1}(\phi)} {r} \, dr}}$

Объяснение:

По теореме площадь ограниченной области $G$ плоскости:

$\boxed{ \boldsymbol{ \displaystyle S = S(G) = \iint\limits_{G} \, dxdy} }$

Область $G:$

$x^{2} + y^{2} = 2x$

$x^{2} + y^{2} = 4x$

$y = x$

$y = 0$

Формула перехода от декартовых к полярным координатам:

$\displaystyle \left \{ {{x = r \cos \phi} \atop {y = r \sin \phi}} \right.$

Запишем функции ограничивающие область $G$ в полярных координатах:

$x^{2} + y^{2} = (r \cos \phi)^{2} + (r \sin \phi)^{2} = r^{2} \cos^{2} \phi + r^{2} \sin^{2} \phi = r^{2}(\cos^{2} \phi + \sin^{2} \phi)=r^{2}$

$r^{2} = 4r \cos \phi \Longrightarrow \boxed{ r = 4 \cos \phi}$

$r^{2} = 2r \cos \phi \Longrightarrow \boxed{ r = 2 \cos \phi}$

Прямая y = 0 образует с осью OX угол 0°.

Пусть $\beta -$ угол, который образует прямая y = x с осью OX.

Так как прямая $y = x$ является биссектрисой в декартовой системе координат, то она делит прямой угол первой и четвертой координатной четверти пополам, то есть $\beta = 90^{\circ} : 2 = 45^{\circ} = \dfrac{\pi}{4}$ .

Таким образом интегрирование будет происходить от кривой $2 \cos \phi$ до кривой $4 \cos \phi$ , а угол будет изменяться от 0 до 0,25π.

$\displaystyle S = \int\limits^{ 0,25\pi} }_{0 } \, d\phi \int\limits^{4 \cos \phi}_{2 \cos \phi} {r} \, dr = \int\limits^{ 0,25\pi} }_{0 } \bigg(\frac{r^{2}}{2} \bigg|^{4 \cos \phi}_{2 \cos \phi} \bigg) \, d\phi = \frac{1}{2} \int\limits^{ 0,25\pi} }_{0 } \bigg( (4 \cos \phi)^{2} - (2 \cos \phi)^{2}\bigg) \, d\phi=$

$\displaystyle = \frac{1}{2} \int\limits^{ 0,25\pi} }_{0 } \bigg( 16 \cos^{2} \phi - 4 \cos^{2} \phi\bigg) \, d\phi= \frac{1}{2} \int\limits^{ 0,25\pi} }_{0 } 12 \cos^{2} \phi \, d\phi =$

$=\displaystyle 6\int\limits^{ 0,25\pi} }_{0 } \frac{1 + \cos 2\phi}{2} \, d\phi=3 \int\limits^{ 0,25\pi} }_{0 } (1 + \cos 2\phi) \, d\phi = 3 \Bigg( \int\limits^{ 0,25\pi} }_{0 } 1 \, d\phi +\int\limits^{ 0,25\pi} }_{0 } \cos 2\phi \, d\phi \Bigg )=$

$\displaystyle = 3 \Bigg( \phi \bigg |^{ 0,25\pi} }_{0} + \frac{1}{2} \int\limits^{ 0,25\pi} }_{0 } \cos 2\phi \, d(2\phi) \Bigg )= 3 \Bigg(( 0,25\pi - 0) + \frac{1}{2} \cdot \sin2\phi \bigg| ^{ 0,25\pi} }_{0} \Bigg) =$

$\displaystyle = 3 \Bigg( \frac{\pi}{4} + \frac{1}{2} \bigg( \sin \bigg(2 \cdot \frac{\pi}{4} \bigg) - \sin(2 \cdot 0) \bigg) \Bigg) = 3 \Bigg( \frac{\pi}{4} + \frac{1}{2} \bigg( \sin \bigg(\frac{\pi}{2} \bigg) - \sin( 0) \bigg) \Bigg) =$

$\displaystyle= 3 \Bigg( \frac{\pi}{4} + \frac{1}{2} \bigg( 1 -0 \bigg ) \Bigg) = \frac{3\pi}{4} + \frac{3}{2} = \frac{3\pi + 6}{4}$ квадратных единиц.