4 завдання , терміново!!!​

Ответ:

1. ОДЗ: х ∈ R.

2. Функция не является четной или нечетной, то есть общего вида.

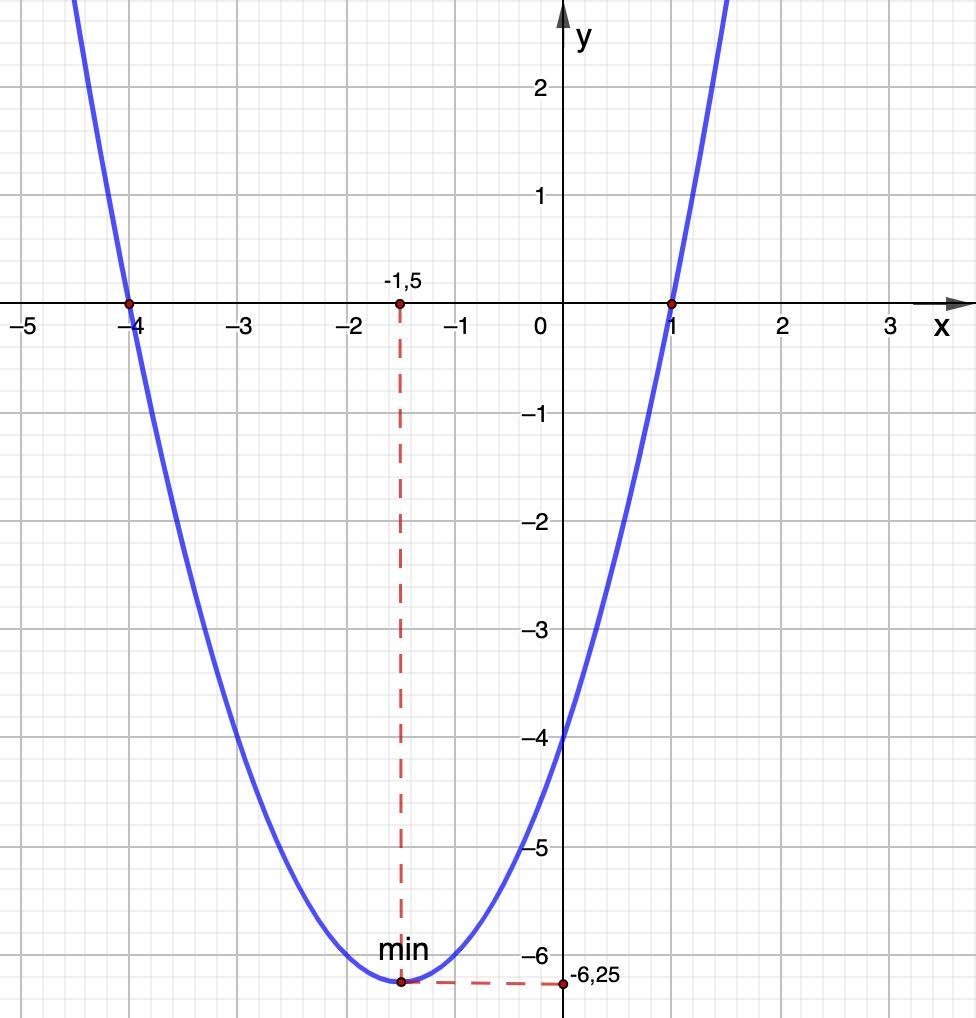
3. 1) х = 0 ⇒ у = -4; 2) у = 0 ⇒ х₁ = -4;   х₂ = 1.

4. Асимптот нет.

5. Функция убывает на промежутке (-∞; -1,5].

Функция возрастает на промежутке [-1,5; +∞).

х min = -1,5.

6. График вогнутый на всем промежутке.

Пошаговое объяснение:

Исследовать функцию и построить график:

f(x) = x² + 3x - 4.

1. ОДЗ: х ∈ R.

2. Четность, нечетность.

Если f(-x) = f(x), то функция четная; если f(-x) = -f(x), то функция нечетная.

f(-x) = (-x)² + 3 · (-x) - 4 = x² - 3x - 4

f(-x) ≠ f(x) ≠ -f(x) ⇒ функция не является четной или нечетной, то есть общего вида.

3. Пересечение с осями.

1) х = 0 ⇒ у = -4;

2) у = 0 ⇒ х² + 3х - 4 = 0

По теореме Виета:

х₁ = -4;   х₂ = 1.

4. Функция непрерывна, асимптот нет.

5. Возрастание, убывание, точки экстремумов.

Найдем производную:

f'(x) = 2x + 3

Приравняем к нулю, найдем корень, отметим его на числовой оси.

Определим знак производной на промежутках. Если ПЛЮС - функция возрастает, если МИНУС - функция убывает.

2х + 3 = 0

х =  -1,5

Функция убывает на промежутке (-∞; -1,5].

Функция возрастает на промежутке [-1,5; +∞).

Если производная меняет знак с МИНУСА на ПЛЮС, то в данной точке будет минимум.

х min = -1,5.

f(-1,5) = -6,25

6. Выпуклость, вогнутость.

Найдем вторую производную:

f"(x) = (f'(x))' = (2x + 3)' = 2

Если производная второго порядка положительна, то график вогнутый.

#SPJ1