Предмет: Математика,
автор: stasok2005
помогите пожалуйста
Приложения:
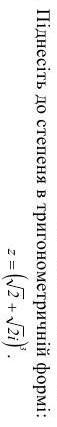
Ответы
Автор ответа:
0
Для возведения комплексного числа в степень, воспользуемся формулой куба
z³ = 2√2 + 6i√2 + 6√2i² + i³2√2
Упрощаем полученное выражение, учитывая, что i² = -1:
z³ = 2√2 + 6i√2 + 6√2(-1) + (-1)i2√2,
z³ = -4√2 + 4i√2.
Модуль этого числа равен √(-4√2)² + (4√2)²) = √(32 + 32) = √64 = 8.
Аргумент для числа во второй четверти равен:
φ = π- arctg(-4√2 / (4√2) = π- arctg(-1) = 3π/4.
Ответ
Комплексное число в 3 степени:
z³ = -4√2 + 4i√2.
Комплексное число в тригонометрической форме записи:
z³ = 8cos(3π /4) + i*sin(3π/4).
Интересные вопросы
Предмет: Русский язык,
автор: 0НеонКА0
Предмет: Русский язык,
автор: Натя44
Предмет: Немецкий язык,
автор: Женяяя11
Предмет: История,
автор: mamedovamariia4227gm
Предмет: Геометрия,
автор: minovaksyushashai