помогите пожалуйста!!!!!!!!!!!!!!!!!!
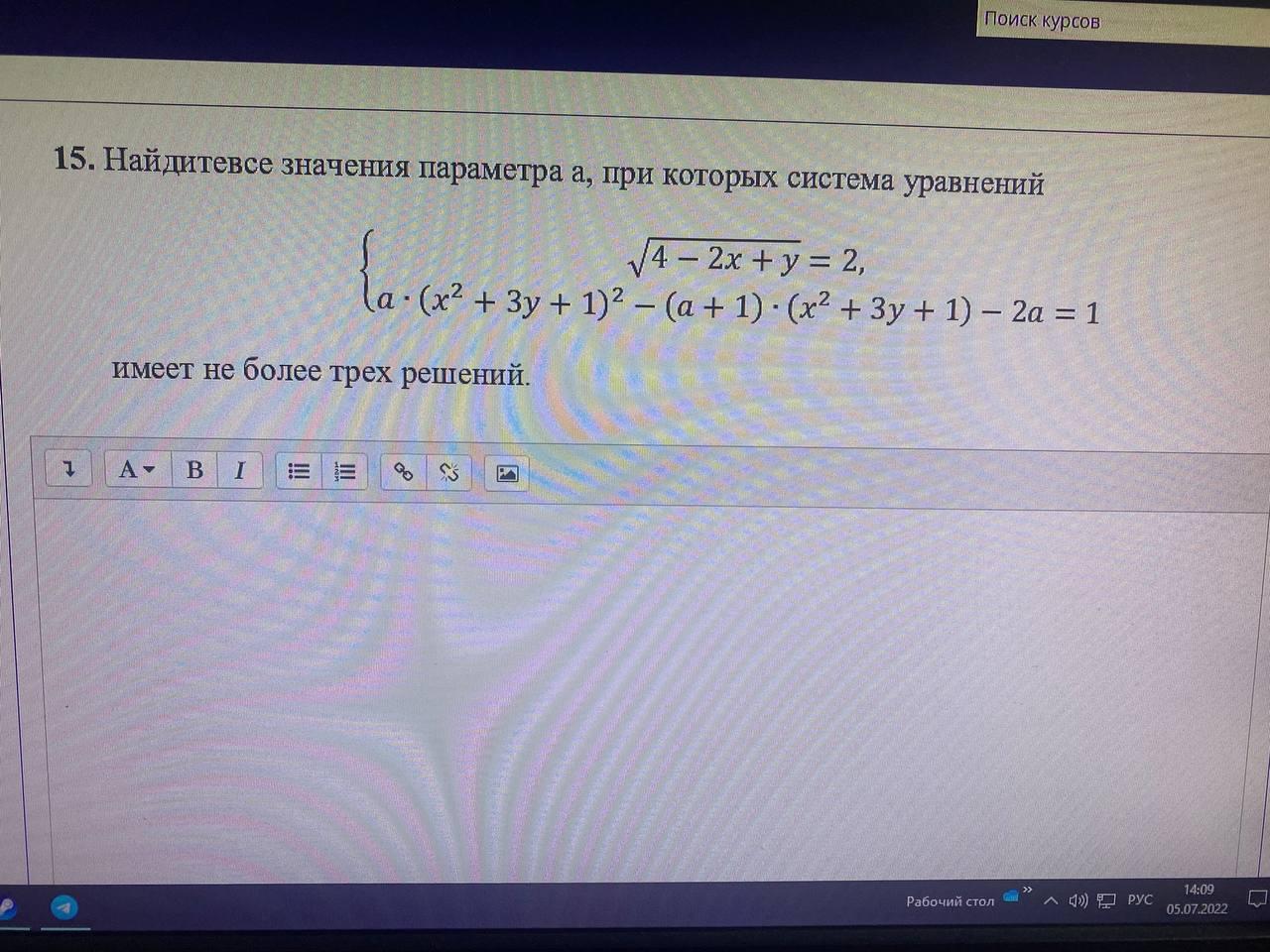
Ответы
Ответ:
При а = -0,1 система уравнений будет иметь 3 корня.
Пошаговое решение:
Выразим с первого уравнения у через х, для этого поднимем левую и правую часть до квадрата:
4-2x+y=4
-2x+y=4-4
-2x+y=0
y=2x
Подставим значение у у второе выражение, получим:
а(х²+6х+1)²-(а+1)(х²+6х+1)-2а=1
Сделаем замену переменных, вместо х²+6х+1 запишем t:
at²-(a+1)²-2a=1
Перенесем 1 влево:
at²-(a+1)²-2a-1=0
У нас получилось квадратное уравнение с коэффициентами
a=a b=-(a+1) c=-2a-1
Найдем дискриминант по формуле D=b²-4ac
D=(-(a+1))²-4*a*(-2a-1)=(a+1)²+4a(2a+1)=a²+2a+1+8a²+4a=9a²+6a+1
По формуле (a+b)²=a²+2ab+b² представим дискриминант по другому:
D=(3а+1)²
Теперь по формулам и
найдем t₁ и t₂:
Возвратимся к замене переменных, получим 2 уравнения:
Решим первое, используя формулы дискриминанта и корней квадратного уравнения:
Как видим, у нас есть 2 разных корня, которые не зависят от а, значит во втором уравнении должен быть только 1 корень. Решим второе уравнение:
С теории про квадратные уравнения известно, что:
- Если D>0 уравнение имеет два корня;
- Если D=0 уравнение имеет один корень;
- Если D<0 уравнение не имеет корней.
Так как нам нужен только один корень, мы должны использовать вариант D=0:
#SPJ1