Предмет: Алгебра,
автор: darks2048
Необходимо найти n. Условие на фото.
Приложения:
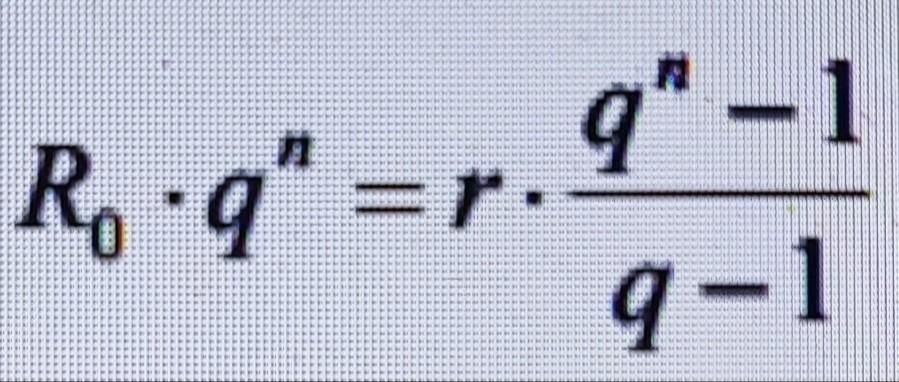
ВикаБач:
R0*q^n -r*q^n/(q-1) = -r/(q-1); q^n*(R0-r/(q-1) = -r/(q-1); q^n = r(1-q) : (R0-r/q-1); Дальше логарифм, ну и "красоту навести".
так я к этому и привел) как дальше логарифм сделать? Типо в основании q, в аргументе то что после тире(справа), ну и этот логарифм равен n ?
да. ну если не требуется какой-то специальный логарифм(двоичный, десятичный, натуральный... тогда ещё коэффициент перехода, а так n=logq(выражение)).
см. ответ
Ответы
Автор ответа:
1
Ответ:
Выразим n из равенства .
Интересные вопросы
Предмет: Русский язык,
автор: andreykaefim
Предмет: Русский язык,
автор: наст55
Предмет: Другие предметы,
автор: dsamoxina
Предмет: Информатика,
автор: andgela2006
Предмет: Математика,
автор: alex37356