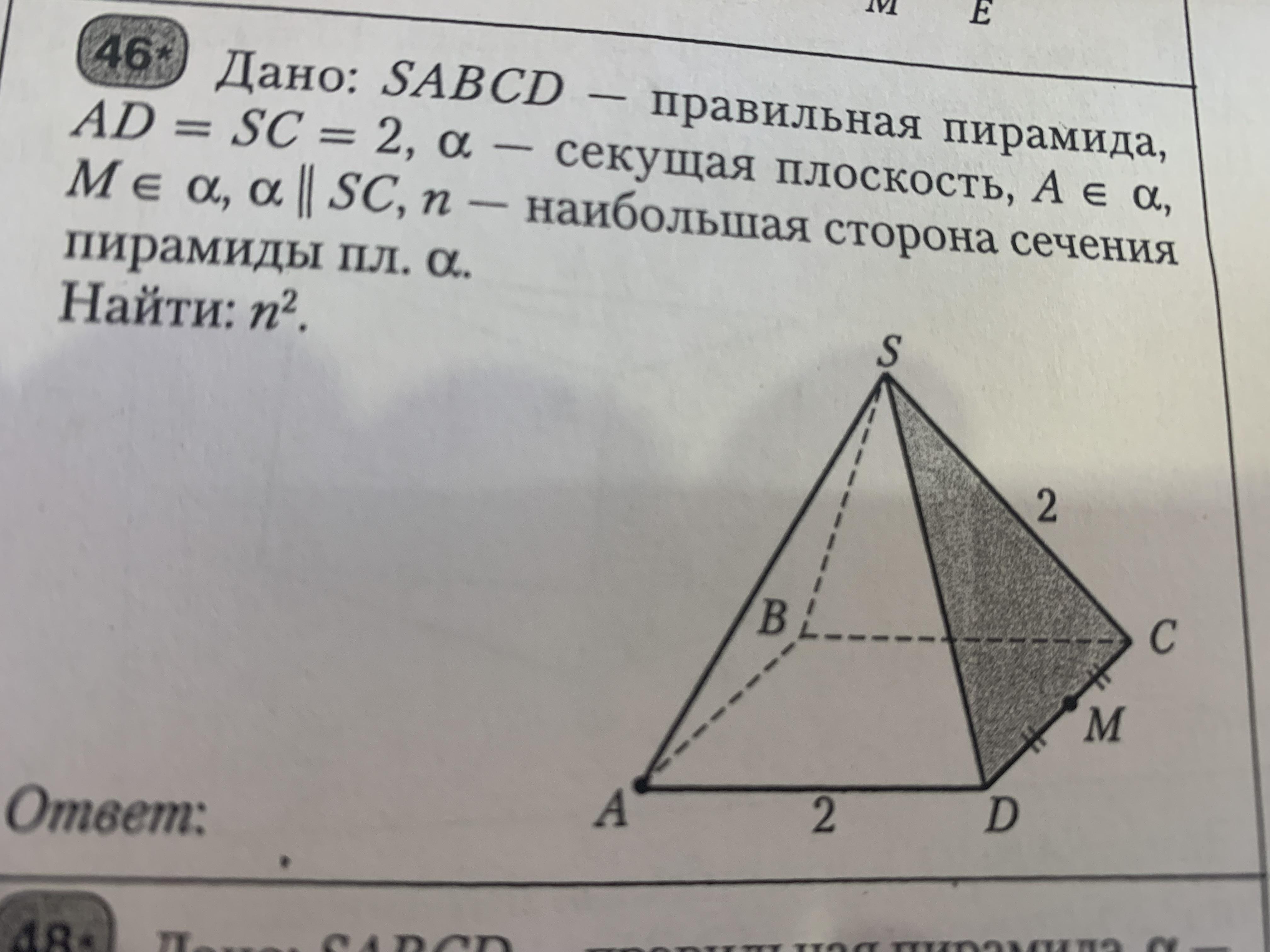
Дано: SABCD - правильная пирамида, AD=SС=2, a - секущая плоскость, А принадлежит а, М принадлежит а, a||SС, n - наибольшая сторона сечения пирамиды пл.a. Найти: n^2

Ответ:

Объяснение:

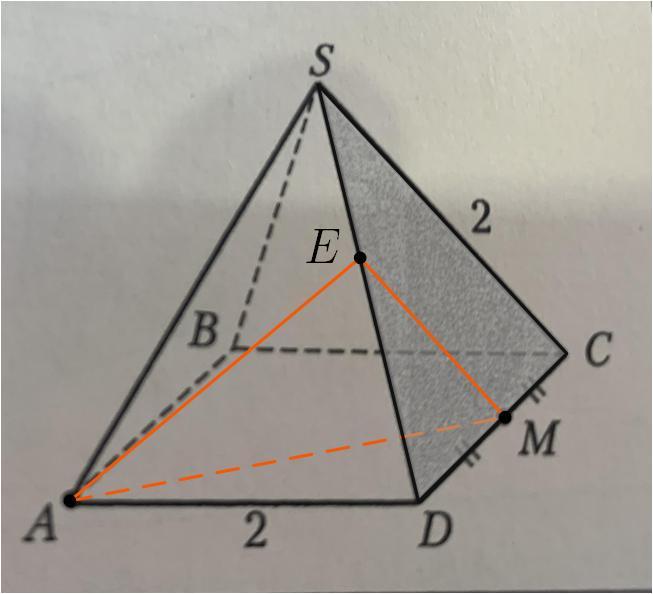
Построим сечение пирамиды, проходящее через точки и параллельно ребру .

Проведем через точку до пересечения с ребром прямую , параллельную ребру . Соединим пары точек, лежащие в одной плоскости: , , .

Сечение пирамиды — треугольник .

Так как пирамида правильная, из условия задачи следует, что все ребра пирамиды равны 2.

— отрезок, проходящий через середину параллельно — средняя линия в треугольнике ,

— медиана в равностороннем треугольнике , а значит и высота. Из треугольника по теореме Пифагора

— отрезок, соединяющий одну из вершин квадрата с серединой несмежной стороны. По теореме Пифагора из треугольника

Среди трех найденных чисел, выражающих длины сторон сечения, самая большая

Тогда