Решить по схеме Горнера
x⁴-x³-13x²+x+12=0;
​

Ответ:

-3; -1; 1; 4

Объяснение:

Находим подбором любые 2 корня уравнения, среди делителей свободного члена

Свободный член (который без x) равен 12

12 делится на ±1; ±2; ±3; ±4; ±6; ±12

Пойдем по порядку: Пусть x=1, тогда

1⁴-1³-13*1²+1+12=0 ⇒ 0=0

Значит x=1 - корень.

Пусть x=-1, тогда

(-1)⁴-(-1)³-13*(-1)²-1+12=0 ⇒ 0=0

Значит x=-1 - корень.

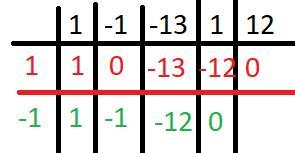
Далее с помощью схемы Горнера понижаем порядок до квадратного уравнения (см. рис.)

x²-x-12=0 ⇒ x₁=-3; x₂=4