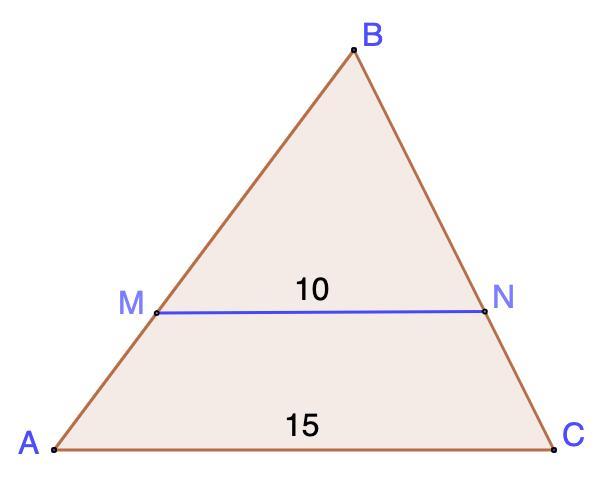
прямая,параллельная сторона АС треугольника АВС , пересекает стороны АВ и ВС в точках M и N соответственно, AC=15, MN=10. Площадь треугольника ABC = 27. Найдите площадь треугольника MBN​

Ответ:

Площадь треугольника MBN​ равна 12 ед.²

Объяснение:

Прямая, параллельная сторона АС треугольника АВС , пересекает стороны АВ и ВС в точках M и N соответственно, AC = 15, MN = 10. Площадь треугольника ABC = 27.

Найдите площадь треугольника MBN​.

Дано: ΔАВС;

MN || AC;

AC = 15, MN = 10;

S(ABC) = 27

Найти: S(MBN).

Решение:

Рассмотрим ΔМВN и ΔАВС.

• Лемма. Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.

⇒ ΔМВN ~ ΔАВС.

• Коэффициент подобия k - это отношение сходственных сторон.

Найдем k:

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Площадь треугольника MBN​ равна 12 ед.².