Предмет: Геометрия,
автор: Аноним
СПАСИТЕ ПОЖАЛУЙСТА!! Мне на завтра!
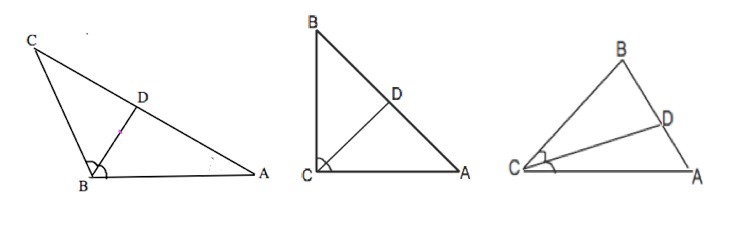
Дано: треугольник ABC
BD - биссектриса
Доказать:
AB>AD
Нужны всевозможные способы!
Ответы
Автор ответа:
0
ВD делит треугольник на две части. Угол АDВ - внешний для ∆ СВD и равен сумме внутренних углов, не смежных с ним (свойство).
Угол АDВ=∠СВD+∠DСВ
Биссектриса делит угол пополам.
Угол АВD=∠СВD. Следовательно,
∠АDВ=∠АВD+∠DСВ⇒
Угол АDВ > угла АВС.
В треугольнике против большего угла лежит большая сторона. ⇒
АВ> АD. Доказанное справедливо как для остроугольного. так и для прямоугольного и тупоугольного треугольника.
Приложения:
Интересные вопросы
Предмет: Физика,
автор: nepluevamaria88
Предмет: Математика,
автор: vonoya9929
Предмет: Математика,
автор: usavenkova13
Предмет: Алгебра,
автор: Mellan