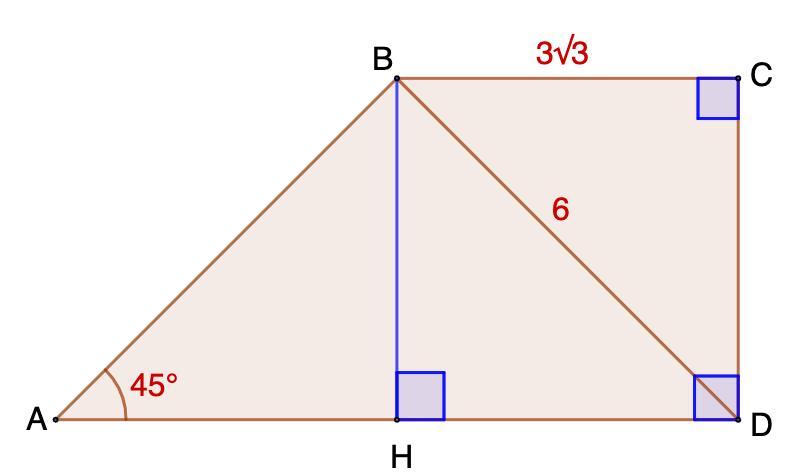
В прямоугольной трапеции ABC с основаниями AD и BC диагональBD равна 6, а угол А равен 45°. Найдите большую боковую сторону, если меньшее основание трапеции равно 3√3

Ответ:

Большая сторона трапеции равна 3√2 ед.

Пошаговое объяснение:

В прямоугольной трапеции ABCD с основаниями AD и BC диагональ BD равна 6, а угол А равен 45°. Найдите большую боковую сторону, если меньшее основание трапеции равно 3√3.

Дано: ABCD - прямоугольная трапеция;

BD = 6 - диагональ;

∠А = 45°;

ВС = 3√3.

Найти: AВ.

Решение:

Проведем высоту ВН.

1. Рассмотрим ΔDBC - прямоугольный.

По теореме Пифагора:

CD² = BD² - BC² = 36 - 27 = 9   ⇒ CD = 3.

2. Рассмотрим HBCD - прямоугольник.

• В прямоугольнике противоположные стороны равны.

⇒ CD = BH = 3.

3. Рассмотрим ΔАВН - прямоугольный.

∠А  = 45°.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠АВН = 90° - 45° = 45°

• Если в треугольнике равны два угла, то этот треугольник равнобедренный.

⇒ АН = НВ = 3

По теореме Пифагора найдем АВ:

АВ² = АН² + НВ² = 9 + 9 = 18 ⇒ АВ = √18 = 3√2

Большая сторона трапеции равна 3√2 ед.