Предмет: Алгебра, автор: kotikula98

ДАЮ 100 БАЛЛОВ! ЗА СПАМ КИДАЮ ЖАЛОБЫ!

Приложения:

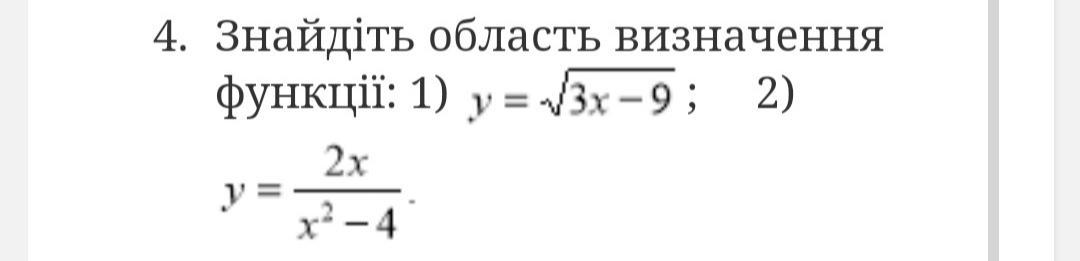
Ответы

Автор ответа: Universalka

3

1)

Подкоренное выражение корня чётной степени должно быть неотрицательным , то есть ≥ 0 .

$\displaystyle\bf\\y=\sqrt{3x-9} \\\\3x-9\geq 0\\\\3x\geq 9\\\\x\geq 3\\\\Otvet \ : \ D(y)=\Big[3 \ ; \ +\infty\Big)$

2)

Знаменатель дроби не должен равняться нулю , так как на ноль делить нельзя .

$\displaystyle\bf\\y=\frac{2x}{x^{2} -4} \\\\x^{2} -4\neq 0\\\\(x-2)(x+2)\neq 0\\\\\\\left \{ {{x-2\neq 0} \atop {x+2\neq 0}} \right. \ \ \ \Rightarrow \ \ \ \left \{ {{x\neq 2} \atop {x\neq -2}} \right. \\\\\\Otvet \ : \ D(y)=\Big(-\infty \ ; \ -2\Big) \ \cup \ \Big(-2 \ ; \ 2\Big) \ \cup \ \Big(2 \ ; \ +\infty\Big)$

Universalka: Спасибо за то , что оценили на "3" .

kotikula98: простите, я случайно нажала.. вы мне очень помогли!!!

kotikula98: с другого аккаунта оценила на 5

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Английский язык, автор: vyfrchdjjdj

6) London is the capital of ...
а) Great Britain only
b) England only
c) Great Britain and England both

1 год назад

Предмет: Математика, автор: annaacina61

Виразити з рівняння x+6y=10 змінну x через замінник y.
ТЕРМІНОВОО

1 год назад

Предмет: Математика, автор: d93308945

Одна із сторiн трикутника 17 см, а друга сторона на 3 см більша за третю. Периметр трикутника 52 см. Скласти рiвняння для розв'язування задачі, якщо через х позначити третю сторону

это очень срочно,это тест на время помогите пожалуйста

1 год назад

Предмет: Математика, автор: butterfly995

представьте в виде многочлена -0,5(6-2y^2)(3+y^2)

7 лет назад

Предмет: Биология, автор: dmitrijvoronec148858

Помогите мне пожалуйста! Тема: "Птицы"!!!
Подберите соответствие:
1). Перелётные птицы
2). Кочующие птицы
3). Оседлые птицы

-сорока, голубь, синица

-перемещение на небольшие расстояния

-журавли, лебеди, ласточки

-перемещение на небольшие расстояния

-миграций не совершают

-грач, серая ворона

7 лет назад