Предмет: Алгебра, автор: nskdoxdkw

40 баллов!!!
Решите интеграл все кроме 1)

Приложения:

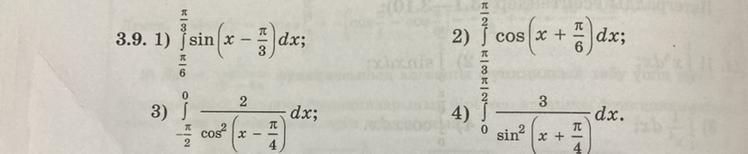
Ответы

Автор ответа: NNNLLL54

Ответ:

Из таблицы интегралов: $\bf \displaystyle \int cos(ax+b)\, dx=\frac{1}{a}\, sin(ax+b)+C\ \ ,$

$\bf \displaystyle \int \frac{dx}{cos^2(ax+b)}=\frac{1}{a}\, tg(ax+b)+C\ ,\ \ \int \frac{dx}{sin^2(ax+b)}=-\frac{1}{a}\, ctg(ax+b)+C$ .

Вычислим определённые интегралы, применяя формулу Ньютона-Лейбница .

$\bf 2)\ \ \displaystyle \int \limits _{\frac{\pi}{3}}^{\frac{\pi }{2}}cos(x+\frac{\pi }{6})\, dx=sin(x+\frac{\pi }{6})\, \Big| _{\frac{\pi}{3}}^{\frac{\pi }{2}}=sin(\frac{\pi }{2}+\frac{\pi }{6})-sin( \frac{\pi}{3}}+\frac{\pi }{6})=\\\\\\=sin\frac{2\pi }{3}-sin\frac{\pi}{2}=\frac{\sqrt3}{2} -1=\frac{\sqrt3-2}{2}$

$3)\ \ \bf \displaystyle \int \limits _{-\frac{\pi}{2}}^0\frac{2}{cos^2(x-\frac{\pi}{4})}\, dx=2tg(x-\frac{\pi }{4})\, \Big|_{-\frac{\pi}{2}}^0=2\cdot \Big(tg(-\frac{\pi}{4})-tg(-\frac{\pi}{2}-\frac{\pi}{4})\Big)=\\\\\\=2\cdot \Big(-1+tg\frac{3\pi }{4}\Big)=2\cdot (-1-1)=-4$

$4)\ \ \bf \displaystyle \int \limits ^{\frac{\pi}{2}}_0\frac{3}{sin^2(x+\frac{\pi}{4})}\, dx=-3ctg(x+\frac{\pi }{4})\, \Big|^{\frac{\pi}{2}}_0=-3\cdot \Big(ctg(\frac{\pi}{2}+\frac{\pi}{4})-ctg\frac{\pi}{4}\Big)=\\\\\\=-3\cdot \Big(ctg\frac{3\pi }{4}-1\Big)=-3\cdot (-1-1)=6$