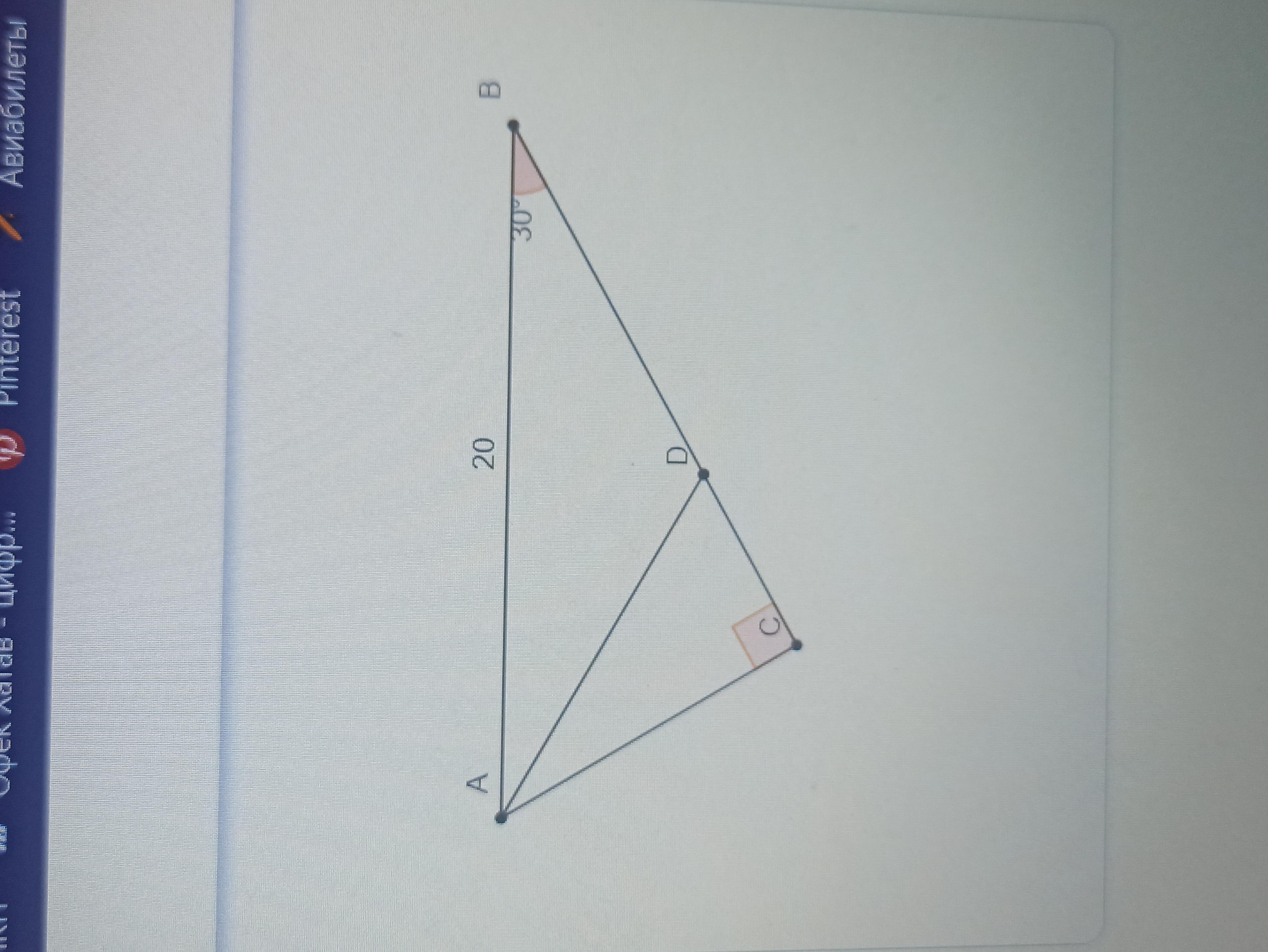
ABC прямоугольный треугольник, 30-60-90, (ACB = 90°)
Дано:
CD - 12 cm.
B - 30°
1. Найдите градусы CAD
2. Найдите длину BC

Ответ:

угол САD=30°, угол АСD=90°, угол ADC=60°, BC=36 см

Объяснение:

AD - бисектриса угла А(угол А=180°-90°-30°=60°), тогда угол CAD= половине угла А=60°÷2=30°;

CD=12 cm (так, как это катет при угле 30°, он равен половине гипотенузы), тогда АD=BD=24 см, угол AВD=угол BAD, как углы при основе.

BC=BD+DC=24cm+12cm=36cm.

Объяснение:

∆АВС - прямоугольный:

катет лежащий против угла 30° равен половине гипотенузы:

АС=АВ:2=20:2=10 см

по теореме Пифагора:

ВС=√(АВ²-АС²)=√(20²-10²)=√300=10√3 см

∆АСD - прямоугольный.

tg∠CAD=CD/AC=12/10=6/5=1,2

∠CAD=50,1944⁰

ответ: ВС=10√3 см; ∠САD=50,1944°

но все же если по условию АD - биссектриса,то

∠BAC=90-∠B=90-30=60°

∠САD=∠BAC:2

=60:2=30⁰

ответ: ВС=10√3 см; ∠САD=30°