Предмет: Математика, автор: Aqmonti

Применяя правила сложения векторов, упростите выражение (RS+ED)-(ND + ES).

Приложения:

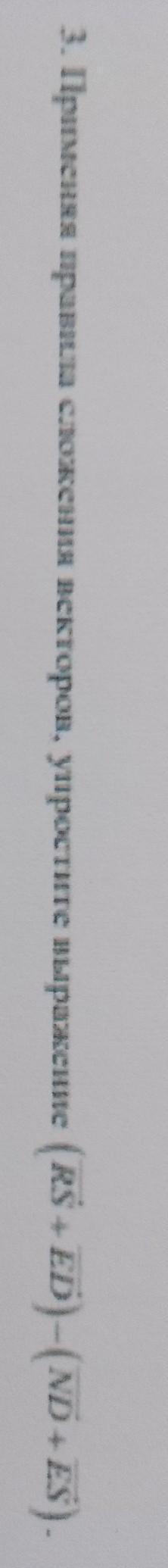
Ответы

Автор ответа: yugolovin

0

Ответ:

$\bar{RN}$

Пошаговое объяснение:

$(\bar{RS}+\bar{ED})-(\bar{ND}+\bar{ES})=\bar{RS}+\bar{ED}-\bar{ND}-\bar{ES}=$

$=\bar{RS}+\bar{ED}+\bar{DN}+\bar{SE}=(\bar{RS}+\bar{SE})+(\bar{ED}+\bar{DN})=$

$=\bar{RE}+\bar{EN}=\bar{RN}.$

Мы воспользовались тем, что

$-(\bar a+\bar b)=-\bar a-\bar b;$

$-\bar{AB}=\bar{BA};$

коммутативность сложения: $\bar a+\bar b=\bar b+\bar a$ ;

ассоциативность сложения: $(\bar a+\bar b)+\bar c=\bar a+(\bar b+\bar c)$ (и поэтому можно скобки вообще не писать: $\bar a+\bar b+\bar c$ ;

$\bar{AB}+\bar {BC}=\bar{AC}.$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Английский язык, автор: hatulechka14

Rewrite the questions in the reported speech.

1. “Where is my umbrella?” she asked.

______________________________________________

2. He asked, “Do I have to do it?”

______________________________________________

3. “Where have you been?” the mother asked her daughter.

______________________________________________

4. “Which dress do you like best?” she asked her boyfriend.

______________________________________________

5. “What are they doing?” she asked.

______________________________________________

6. “Are you going to the cinema?” he asked me.

______________________________________________

7. “Where will you live after graduation?” Jenny wondered.

______________________________________________

8. “Have you been to Italy?” children asked.

______________________________________________

9. “Where do your parents live?” Elizabeth wondered.

______________________________________________

10. “What do the children study on Fridays?” she asked the teacher.

______________________________________________

1 год назад

Предмет: История, автор: antonavick

Виправте історичні помилки в тексті.
У XIVст. відбулося закріпачення українського селянства. У цей час
поширюється велике землеволодіння, яке називають копним. Щоб
розширити свої володіння, землевласники відбирали церковні землі.
Більшість великих господарств були фільварковими, тобто виробляли
продукцію для особистого споживання.

1 год назад

Предмет: Биология, автор: VictoriaVV14

Порівняйте особливості застосування методів селекції рослин, тварин та мікроорганізмів

1 год назад

Предмет: Математика, автор: Kirillak24

решите уравнение a)1.2(5-x)-1.8 (x+4)=-4.2
б) 2/1/7 x - 3/9/14 x + x =-3

7 лет назад

Предмет: Русский язык, автор: hfdhhf

- Имя прилагательное - это __________________________________________
- которая обозначает ________________________________________________
- отвечает на вопросы _______________________________________________
- в предложении является ___________________________________________
- в начальной форме отвечает на вопрос ______________________________

Имя прилагательное изменяется по _________________________

Приведи примеры имен прилагательных
__________________________________________________________________

7 лет назад