В равнобокой трапеции длина боковой стороны 20 мм, длины оснований 5 см и 7 см.

1)Найдите периметр трапеции в см.
2)Найдите градусную меру меньшего угла трапеции.
3)Найдите градусную меру большего угла трапеции.

Ответ:

1) периметр трапеции равен 16 см

2) градусная мера меньшего угла трапеции равна 60°

3) градусная мера большего угла трапеции равна 120°

Объяснение:

В равнобокой трапеции длина боковой стороны 20 мм, длины оснований 5 см и 7 см.

1)Найдите периметр трапеции в см.

2)Найдите градусную меру меньшего угла трапеции.

3)Найдите градусную меру большего угла трапеции.

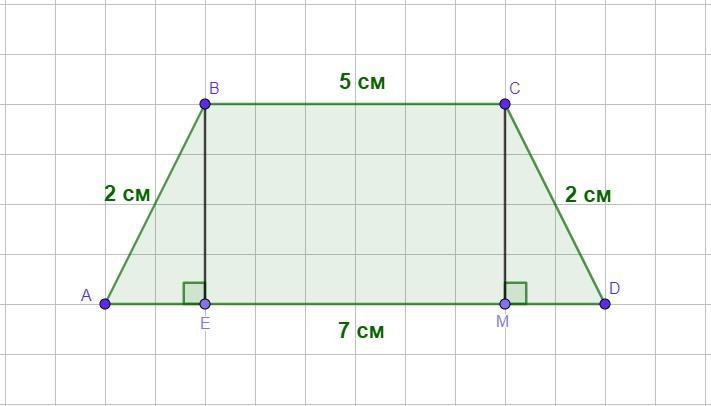
Дана трапеция ABCD, АВ=CD=20 мм = 2 см, ВС=5 см, АD=7 см

1) Найдём периметр трапеции.

• Периметр трапеции равен сумме 4-х её сторон:

Р(ABCD)=AB+ВС+CD+АD=2+5+2+7=16 (см)

2) Найдём градусную меру меньшего угла трапеции (∠А-?)

Из вершины В к основанию АD проведём высоты ВЕ и СМ. Рассмотрим четырёхугольник ВСМЕ.

Так как все углы четырёхугольника прямые по построению, то ВСМЕ - прямоугольник, поэтому ЕМ=ВС= 5 (см) - по свойству прямоугольников.

Рассмотрим прямоугольные треугольники АВЕ и DСМ.

АВ=CD - по условию,

ВЕ=СМ - как высоты трапеции.

⇒ΔАВЕ = ΔDСМ по катету и гипотенузе.

Из равенства треугольников следует равенство сторон: АЕ=МD

Таким образом:

 (см)

Рассмотрим прямоугольный ΔАВЕ.

Гипотенуза АВ=2см, катет АЕ=1 см.

• Если в прямоугольном треугольнике катет равен половине гипотенузы, то он лежит против угла в 30°.

Таким образом ∠АВЕ=30°

Так как сумма острых углов прямоугольного треугольника равна 90°, то ∠ВАЕ=90°-∠АВЕ=90°-30°=60°

Итак, градусная мера меньшего угла трапеции равна 60° (∠А=60°).

3) Найдём градусную меру большего угла трапеции (∠В-?)

Так как сумма углов, прилежащих к боковой стороне, равна 180 ° , то:

∠В=180°-∠А=180°-60°=120°

Градусная мера большего угла трапеции равна 120° (∠В=120°)

#SPJ1