Предмет: Алгебра, автор: chiefsurkov1

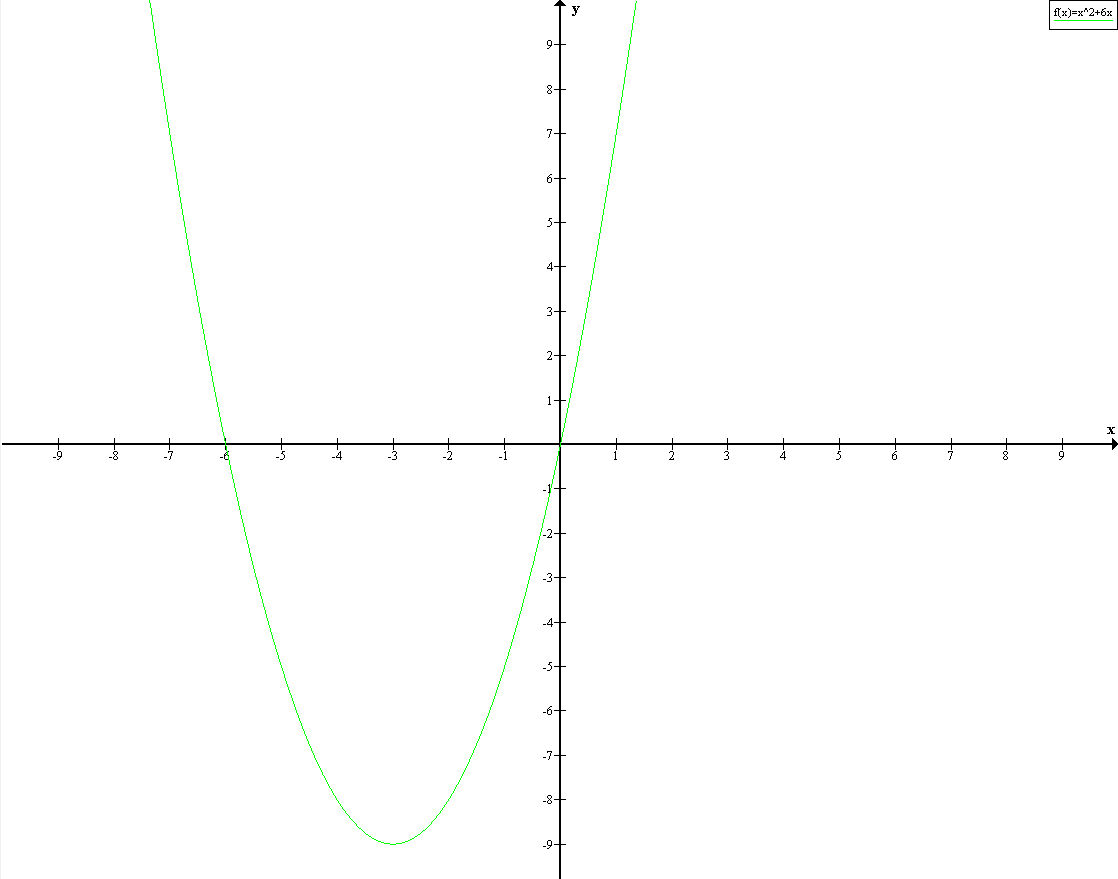
1. постройте график функции y=x^2+6x. Я вот не знаю как его строить.
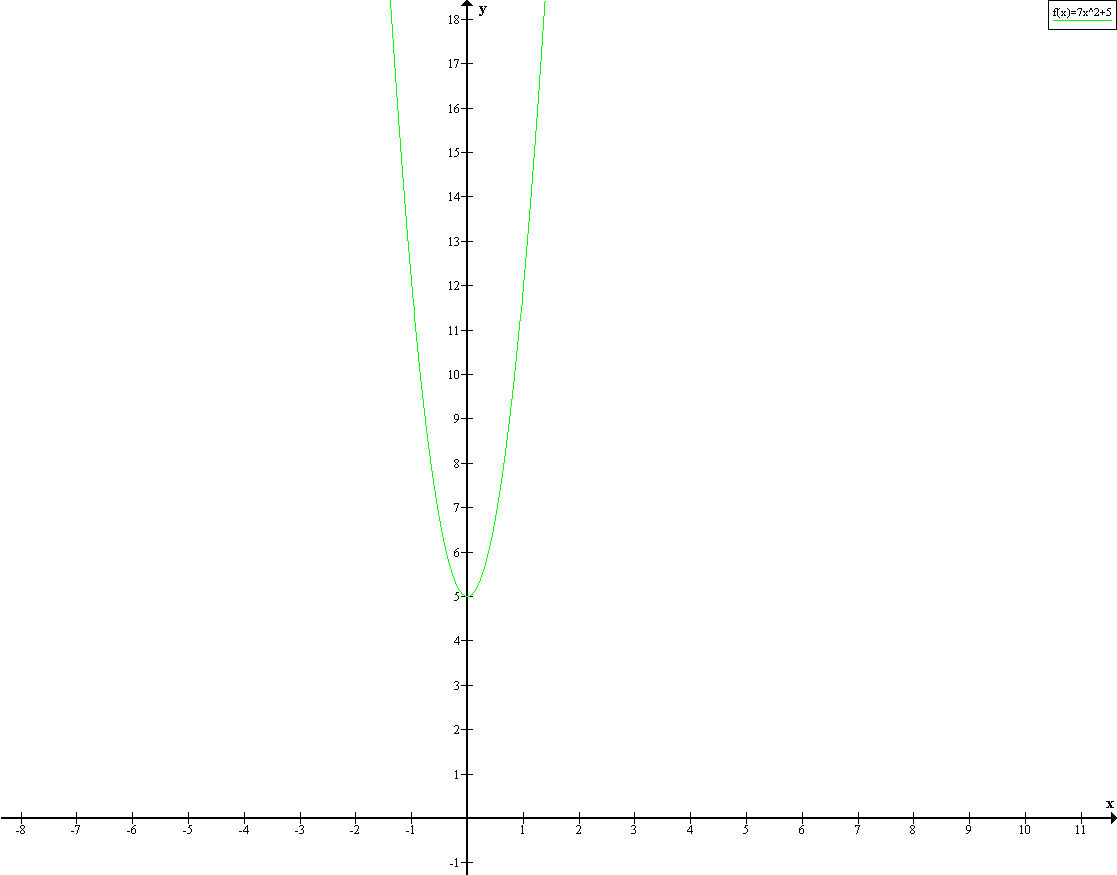
2. Докажите, что функция y=7x^2+5 убывает на промежутке (-бесконечность; 0)

Ответы

Автор ответа: mailforazi

0

1. график в приложении
$y'=2x+6 \ 2x+6=0 \ 2x=-6 \ x=-3 \ \ y(-3)=(-3)^2+6(-3)=9-18=-9$
(-3;-9) - вершина параболы
$x^2+6x=0 \ x(x+6)=0 \ x_1=0 \ x_2=-6$
0 и -6 - точки по оси Х, где график пересекает ось Х

2. график тоже в приложении
$y'=14x \ 14x=0 \ x=0$

- +
--------------|----------------->x
0
0 - нижняя точка перегиба графика (минимум)

левее 0 в производной знак "-", поэтому на участке $(-infty;0)$ функция убывает

Приложения:

Автор ответа: chiefsurkov1

0

как вы определили, что так нужно строить пеервый график? какие преобразования делали?

Автор ответа: mailforazi

0

ладно, щас распишу, а так ... это программа сама сделала, я только функцию написал :D

Автор ответа: chiefsurkov1

0

Может я тупой, но тут же график y=x в квадрате+6x, а у тебя 2икс плюс 6

Автор ответа: mailforazi

0

ну так мы же производную берем что бы найти координату х вершины параболы

Автор ответа: chiefsurkov1

0

кароч, спасибо. Наставил меня на верный путь, сейчас сам все понял

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Физика, автор: Рассазы

А)почему при одинаковом размере помещений радиатор парового отопления имеет меньше секций, чем радиатор водяного отопления?
Б) пар, поступающий в радиатор парового отоплкния, имеет ту же температуру, что и вода, покидающая радиатор, происходит ли при этом обогрев комнаты?

6 лет назад

Предмет: Математика, автор: karfidovandrei

задания №9.1, №9.2, №9,3, №9.4

6 лет назад

Предмет: Қазақ тiлi, автор: gachapoor

ҮЙ ТАПСЫРМАСЫ:
«Қара ниет» «ашық мінез», «тәтті кәмпит», «кара
көйлек» сөздеріне бір-бір сөйлемнен құраңыз, кандай
мағына беріп тұрғандығын табыңыз.

6 лет назад

Предмет: Алгебра, автор: Diman64rus

Найдите наименьший корень уравнения (2х+7)(х-2)=0 с решением пожалуйста

10 лет назад

Предмет: Алгебра, автор: Эммма

. Укажите множество значений функции y=9+3cos5x

10 лет назад