Предмет: Математика, автор: terrorist20083

Найдите определенный интеграл

Приложения:

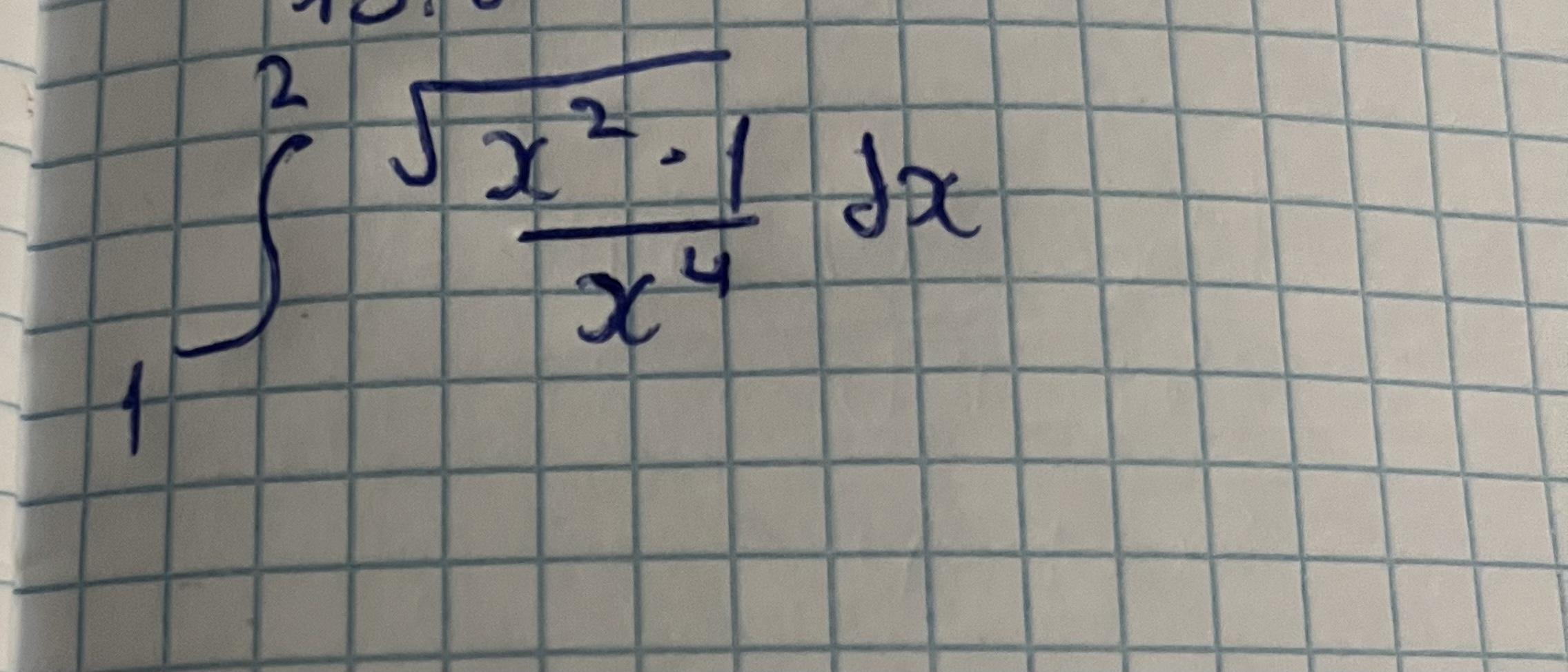
Ответы

Автор ответа: NNNLLL54

1

Ответ:

Найдём сначала неопределённый интеграл . Применяем тригонометрическую подстановку .

$\displaystyle \int \frac{\sqrt{x^2-1}}{x^4}\, dx=\Big[\ x=\dfrac{1}{cost}\ ,\ dx=\frac{sint}{cos^2t}\, dt\ ,\ \sqrt{x^2-1}=\sqrt{\dfrac{1}{cos^2t}-1}=\\\\\\=\sqrt{tg^2t}=tgt\ ,\ t=arccos\frac{1}{x}\ \Big]=\int \frac{tgt}{\frac{1}{cos^4t}}\cdot \frac{sint}{cos^2t}\, dt=\\\\\\=\int \frac{sint\cdot cos^4t}{cost}\cdot \frac{sint}{cos^2t}\, dt=\int sin^2t\cdot cost\, dt=\frac{sin^3t}{3}+C=\\\\\\=\frac{1}{3}\cdot sin^3\Big(arccos\frac{1}{x}\Big)+C\ ;$

$\displaystyle \int \limits_1^2\frac{\sqrt{x^2-1}}{x^3}\, dx=\frac{1}{3}\, sin^3\Big(arccos\frac{1}{x}\Big)\, \Big|_1^2=\frac{1}{3}\cdot \Big(sin^3(arccos1)-sin^3(arccos\frac{1}{2})\Big)=\\\\\\=\frac{1}{3}\cdot \Big(sin^30-sin^3\frac{\pi }{3}\Big)=\frac{1}{3}\cdot \Big(0-\Big(\frac{\sqrt3}{2}\Big)^3\Big)=-\frac{1}{3}\cdot \frac{3\sqrt3}{8}=\bf -\frac{\sqrt3}{8}$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Окружающий мир, автор: zalevskijveniamin8

Хто з дітей має рацію?

Марина

Артем

Ніхто

Усі мають рацію

1 год назад

Предмет: Русский язык, автор: markkukanov5

помогите пожалуйста дам 40 баллов

1 год назад

Предмет: Физика, автор: lerok3120

Куля масою 0,5 г влучає в підвішений на стрижнях дерев'яний брусок масою 300 г і застрягає в ньому. Визначте, з якою швидкістю рухалася куля, якщо після влучення кулі брусок піднявся на висоту 1,25 см

1 год назад

Предмет: Математика, автор: matveyguben

Сначала реши задачу по действиям,потом составь выражение.
На борт космического корабля погрузили 200 тюбиков по 250 г борща для дальнего полёта.Их распределили в несколько лотков поровну в каждый.Когда из одного лотка израсходовали 5 кг,в нём осталось ещё 35 кг.
Сколько лотков с борщом загрузили.
Пж помогите !!!!!!!!!!!!!!!!!!
Даю 67 БАЛЛОВ

7 лет назад

Предмет: Литература, автор: ayazhanzhomartkanova

помогите пожалуйста

7 лет назад