Предмет: Геометрия, автор: zmeura1204

Чертеж на фотографии. Найти угол х.

Приложения:

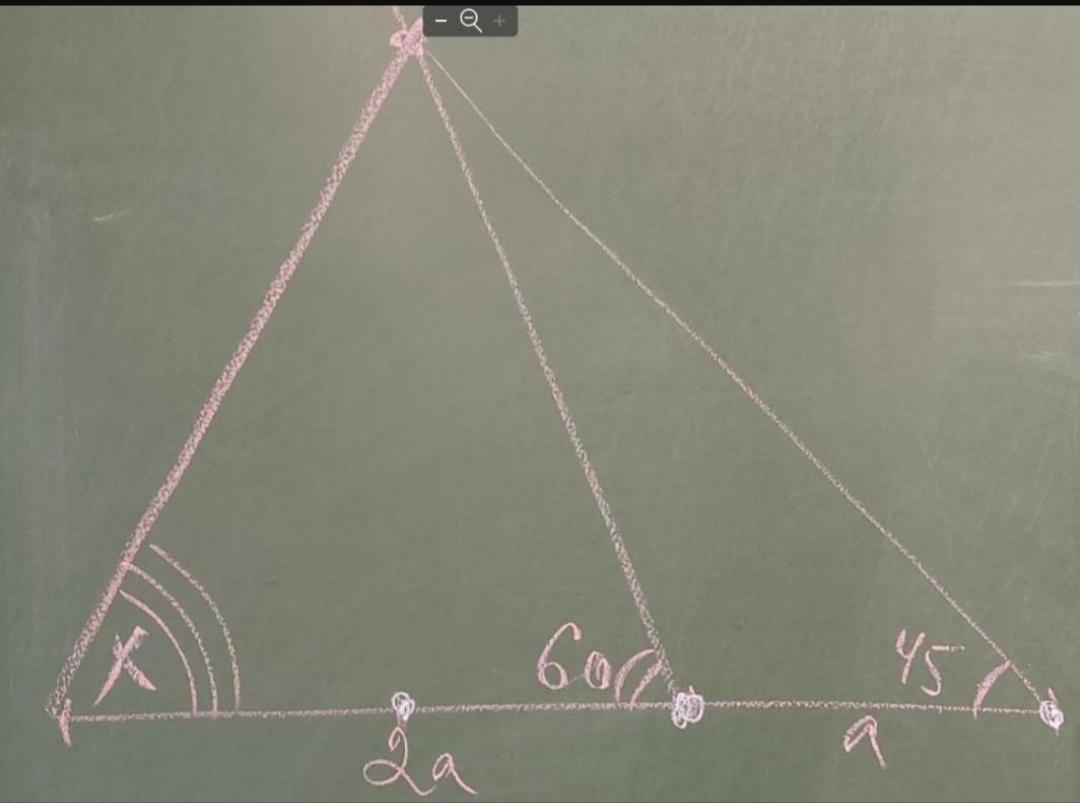
alinkaamaalinkaa48: 70?

zmeura1204: Нет.

alinkaamaalinkaa48: Тогда хз. Просто у треугольника всего 180°, а 60+45 =110. 180-110 =70

Ответы

Автор ответа: flybirdster

Ответ: 75°

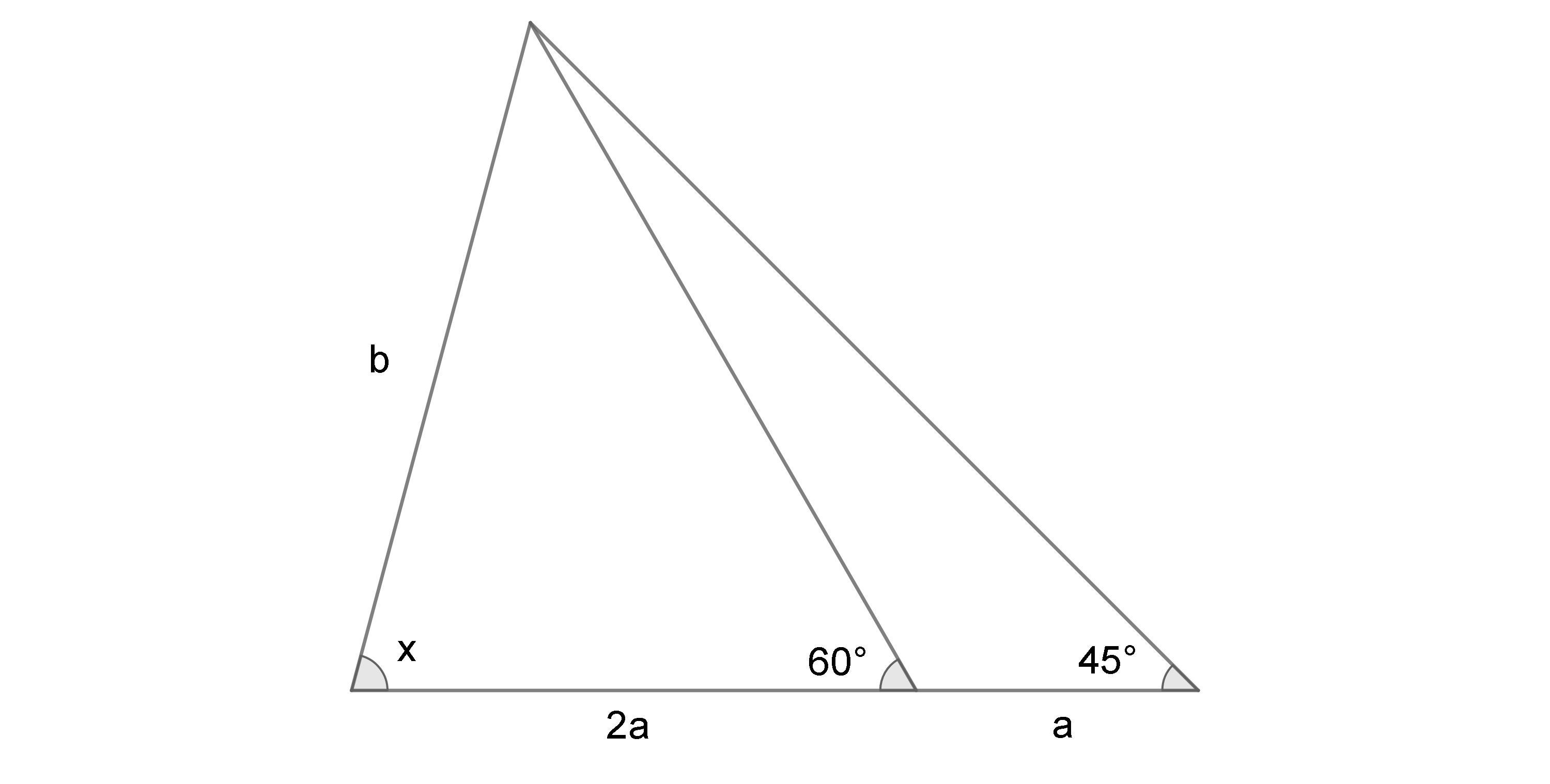
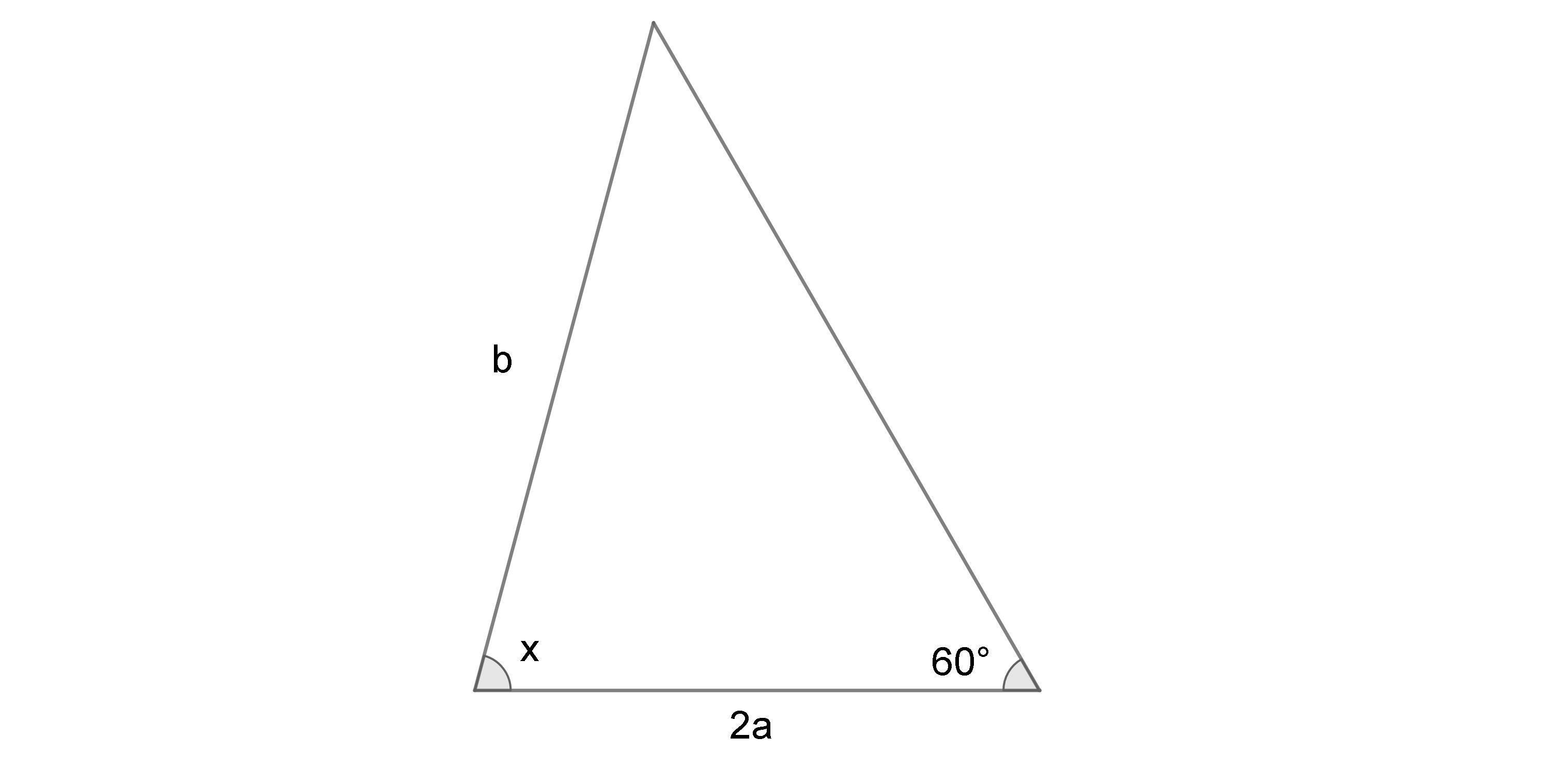
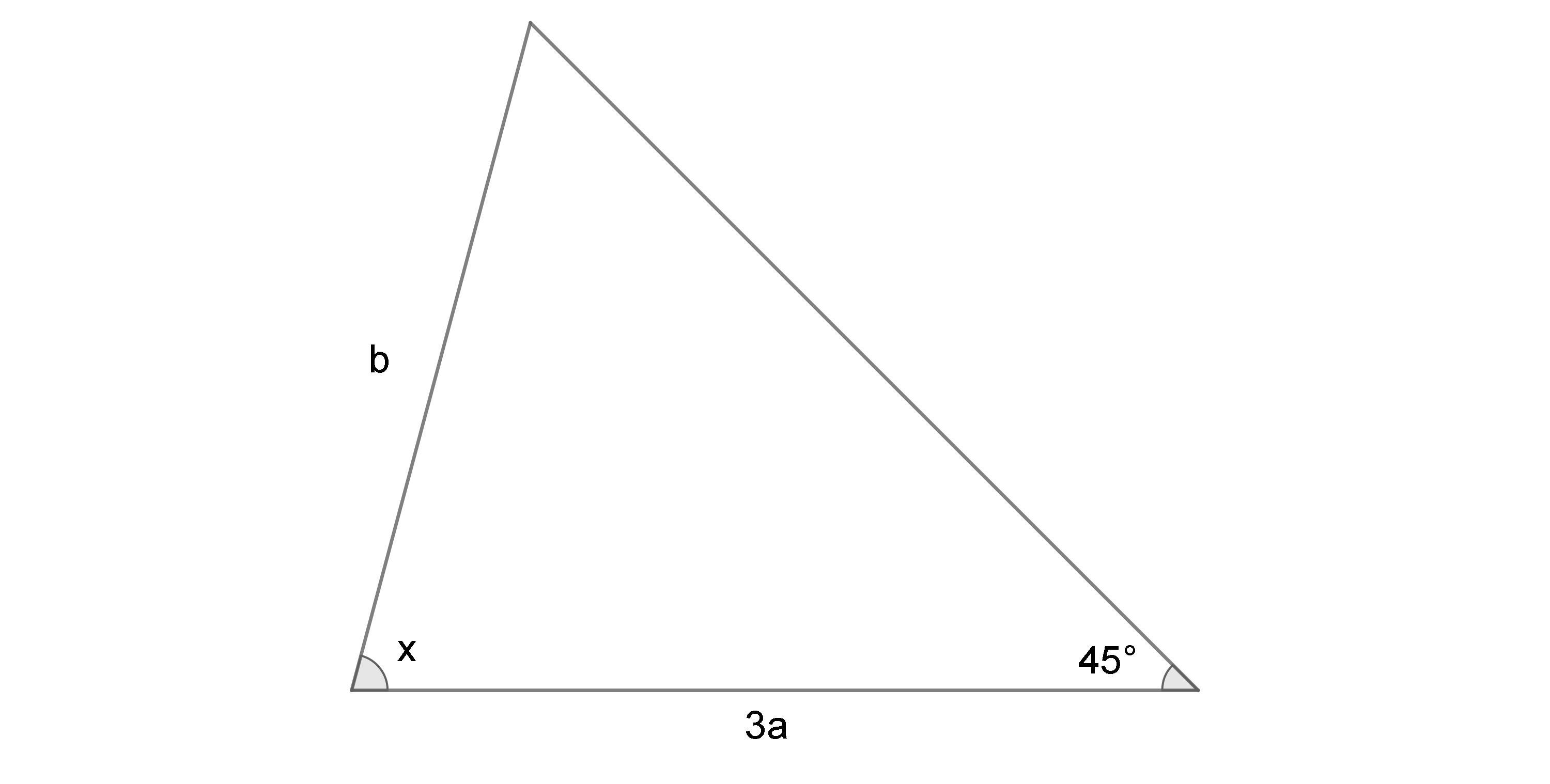
Решение с объяснением: у нас есть два треугольника. Один с основанием 2а, другой с основанием 2а + а = 3а. У них имеются одна общая сторона. Обозначим ее как b.

Найдем углы, противолежащие сторонам 2а и 3а:

$\alpha _{2a} =180-60-x$ ⇒ $\alpha _{2a} =120-x$

$\alpha _{3a}=180-45-x$ ⇒ $\alpha _{3a}=135-x$

Теперь, пользуясь теоремой синусов, для каждого треугольника составим уравнение:

$\frac{b}{sin60} =\frac{2a}{sin\alpha _{2a}}$ ⇒ $b=\frac{2a}{sin\alpha _{2a}} *sin60$

$\frac{b}{sin45} =\frac{3a}{sin\alpha _{3a}}$ ⇒ $b=\frac{3a}{sin\alpha _{3a}} *sin45$

Приравняем их:

$\frac{2a}{sin\alpha _{2a}} *sin60=\frac{3a}{sin\alpha _{3a}} *sin45$

$\frac{2a}{sin(120-x)} *\frac{\sqrt{3} }{2} =\frac{3a}{sin(135-x)} *\frac{\sqrt{2} }{2}$

Обе части умножаем на 2/a:

$\frac{2\sqrt{3} }{sin(120-x)} =\frac{3\sqrt{2} }{sin(135-x)}$

Через пропорцию получим:

$2\sqrt{3} sin(135-x)=3\sqrt{2} sin(120-x)}$

$\sqrt{2} sin(135-x)=\sqrt{3} sin(120-x)}$

Пользуясь формулой вычитания, раскрываем синусы:

$\sqrt{2} (sin135*cosx-cos135*sinx)=\sqrt{3} (sin120*cosx-cos120*sinx)$

$\sqrt{2} (\frac{\sqrt{2} }{2} cosx-(-\frac{\sqrt{2} }{2} )sinx)=\sqrt{3} (\frac{\sqrt{3} }{2} cosx-(-\frac{1}{2} )sinx)$

$\sqrt{2} (\frac{\sqrt{2} }{2} cosx+\frac{\sqrt{2} }{2} sinx)=\sqrt{3} (\frac{\sqrt{3} }{2} cosx+\frac{1}{2} sinx)$

$cosx+sinx=\frac{3}{2} cosx+\frac{\sqrt{3} }{2} sinx$

$\frac{3}{2} cosx-cosx+\frac{\sqrt{3} }{2} sinx-sinx=0$

$(\frac{3}{2} -1)cosx+(\frac{\sqrt{3} }{2} -1)sinx=0$

$\frac{1}{2} cosx+\frac{\sqrt{3} -2}{2} sinx=0$

Обе части умножаем на 2 и делим на косинус икса:

$cosx+(\sqrt{3} -2}) sinx=0$

$1+(\sqrt{3} -2}) tgx=0$

Найдем тангенс угла:

$(\sqrt{3} -2}) tgx=-1$

$tgx=-\frac{1}{\sqrt{3} -2}} }$

$tgx=-\frac{1}{\sqrt{3} -2}*\frac{\sqrt{3} +2}{\sqrt{3} +2}}$

$tgx=-\frac{\sqrt{3} +2}{3-4}$

$tgx=\sqrt{3} +2$

Найдем угол х:

$x=arctg(\sqrt{3} +2)$

$x=75$

Угол х равен 75°.

Приложения:

mmmrks1212: Здравствуйте! Можете пожалуйста зайти ко мне в профиль, вы раньше уже помогли мне с решением задачи. Если вас не затруднит, ответьте пожалуйста на мой последний вопрос, даю 30 баллов. Уже 3 дня никто не отвечает.

zmeura1204: А без тригонометрии?