В основі піраміди , висота якої 8 см лежить прямокутний трикутник. Усі бічні ребра піраміди рівні . Знайти бічне ребро піраміди , якщо найбільша сторона основи дорівнює 12 см

Ответ:

бічне ребро піраміди дорівнює 10см

Объяснение:

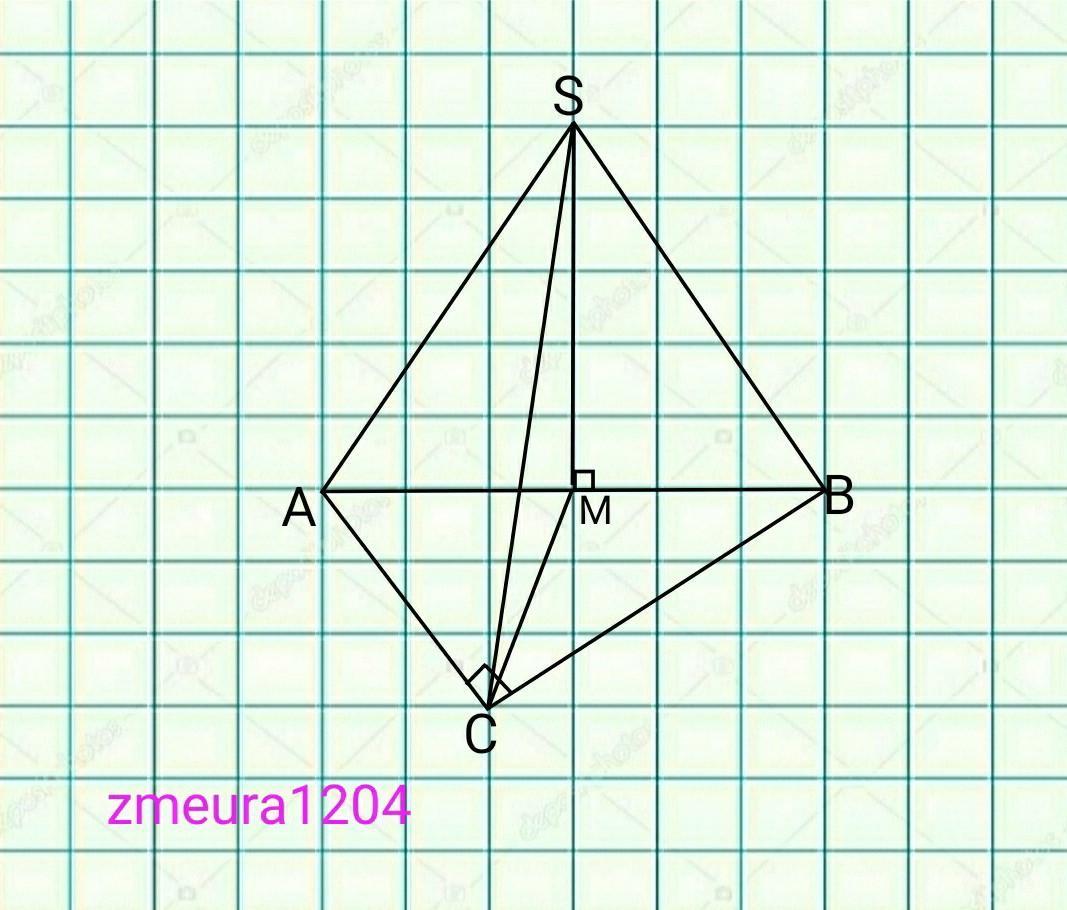
∆ABC- прямокутний трикутник

∠АСВ=90°

АВ=12см гіпотенуза.

SM=8см висота.

SB=SA=SC=?

_________

Розв'язання:

Усі ребра рівні, тож вершина проектується в середину гіпотенузи.

АМ=МВ.

МВ=АВ/2=12/2=6см

∆SMB- прямокутний трикутник

За теоремою Піфагора:

SB=√(SM²+MB²)=√(6²+8²)=10см