5. Основанием пирамиды ABCDF является параллелограмм ABCD, M — точка A.
есть проекция на BD. Известно, что BF = DF. Докажите, что расстояние от точки M до середины AF равно половине CF.

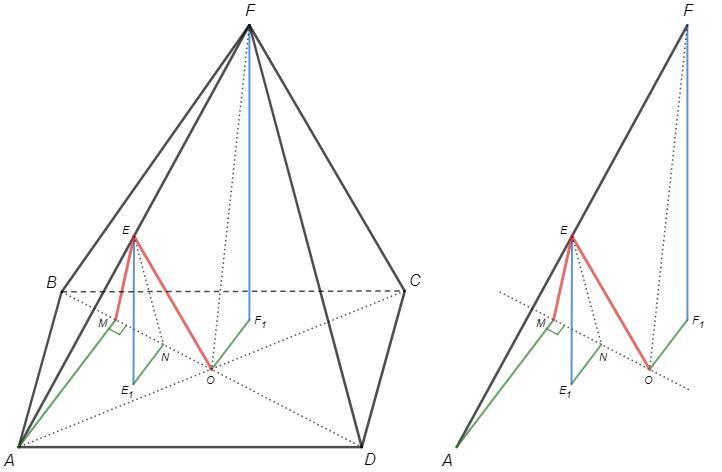
E - середина AF, O - середина BD (точка пересечения диагоналей параллелограмма ABCD)

OE - средняя линия △CAF, OE=CF/2

Докажем, что ME=OE

△BFD -р/б, FO⊥BD (высота/медиана)

Спроецируем отрезки AE и EF сначала на плоскость основания, затем на прямую BD

EN⊥BD и OF1⊥BD (по т о трех перпендикулярах)

AE → AE1 → MN

EF → E1F1 → NO

Отрезки равны - их проекции равны, MN=NO

EN - высота/медиана => △MEO -р/б, ME=OE =CF/2