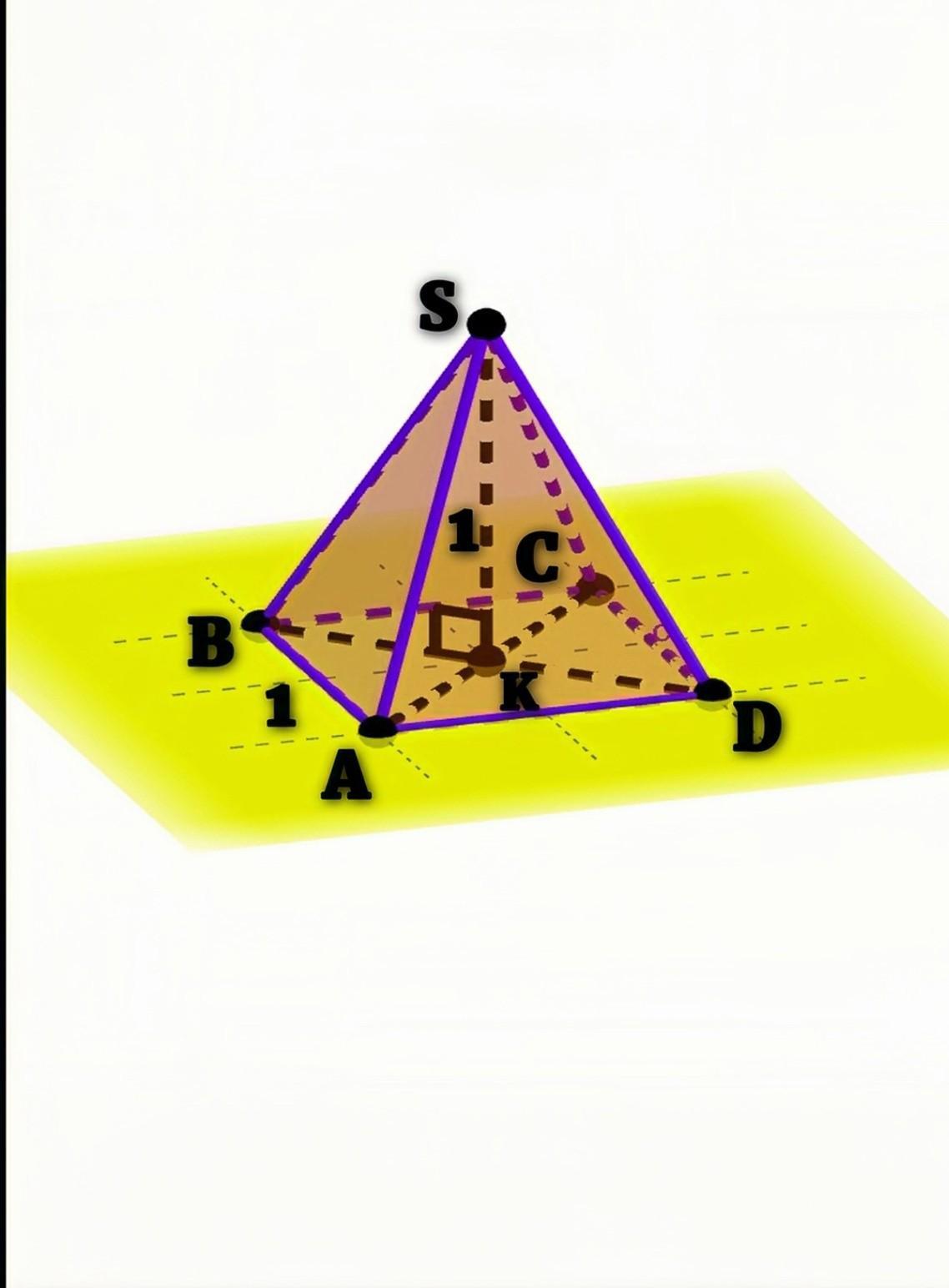
Для правильной четырехугольной пирамиды SABCD, стороны основания и высота которой равны 1 см, найдите расстояние от точки В до плоскости SAC.​

Дано: SABCD - правильная четырехугольная пирамида, АВ = 1см, SK = 1см, ВК ⟂ (АВС)

Найти: Р(В;(SAC))

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение

• Проведем диагональ АС и получим плоскость (SAC).
• Расстояние от точки до плоскости – это длина перпендикуляра, опущенного из данной точки на плоскость.
• Из вершины В опустим перпендикуляр на плоскость (SAC). Р(В;(SAC)) = BK.
• Проведем ещё диагональ BD. ВК - это половина диагонали BD. Сторона квадрата известна, тогда ВD = 1 * √2 = √2 ⇒ВК = √2/2см

Ответ: Р(В;(SAC)) = √2/2см