Предмет: Математика, автор: zsdss

УМОЛЯЮ РЕШИТЕ!!!
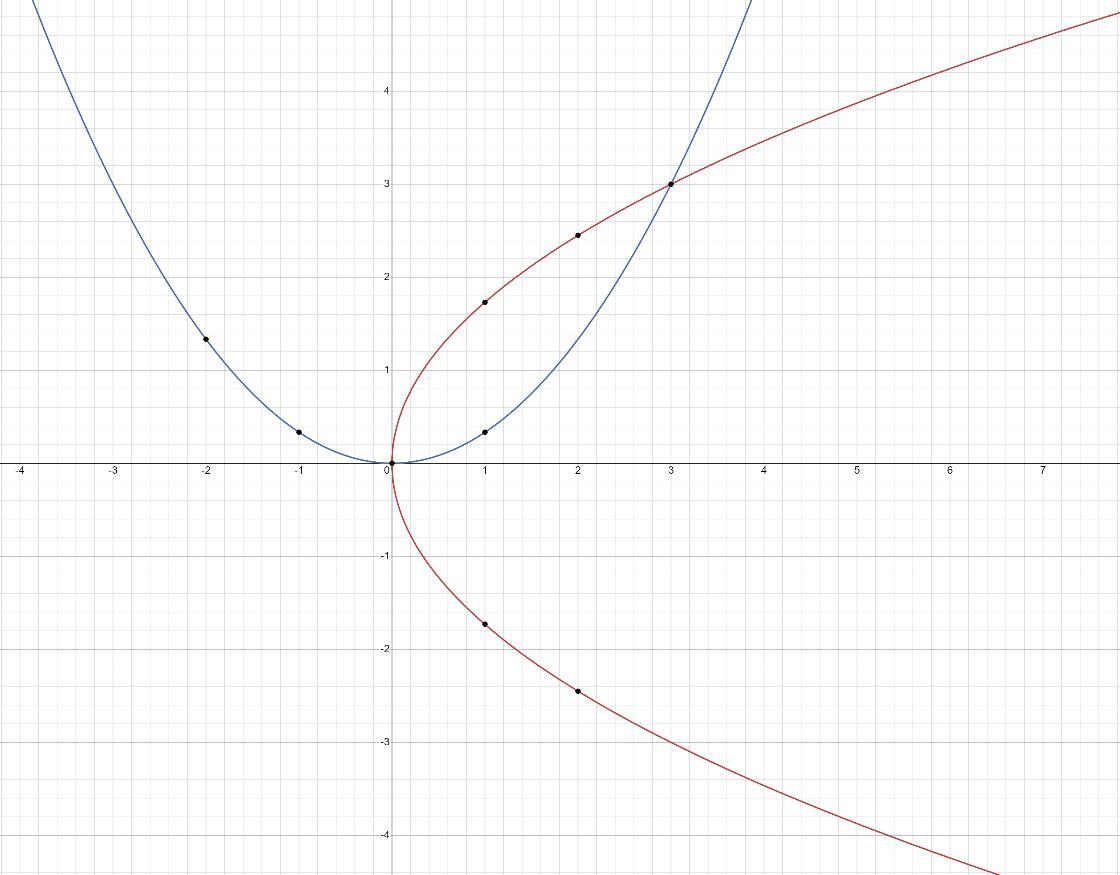
1) Построен график x^2=3y, y^2=3x (на картинке)
а) Найти S данной плоской фигуры
б) Найти V тела, образованного вращением этой фигуры вокруг оси Ox
Для нахождения S и V тела использовать определенный интеграл исходя из данных x и y

Приложения:

Ответы

Автор ответа: NNNLLL54

Ответ:

1) Формула площади криволинейной трапеции:

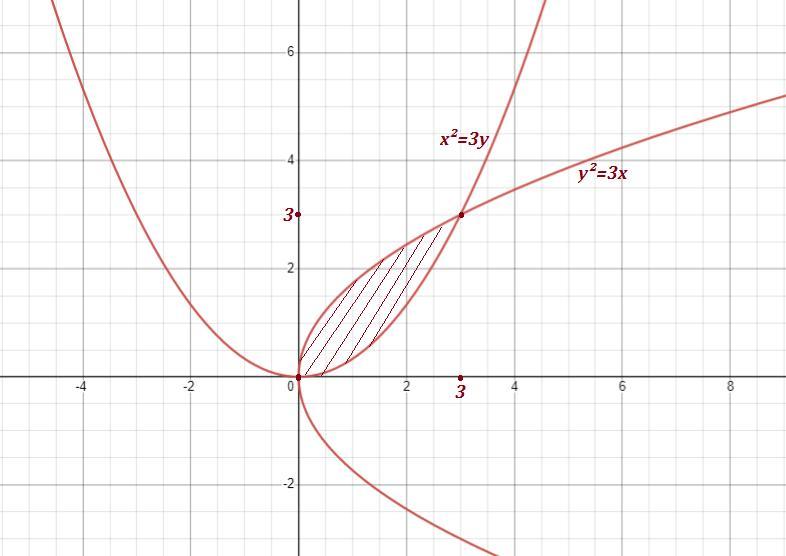
$\bf \displaystyle S=\int\limits_{a}^{b}\, f(x)\, dx$ .

Найдём точки пересечения парабол x²=3y , y²=3x .

$\left\{\begin{array}{l}\bf x^2=3y\\\bf y^2=3x\end{array}\right\ \ \left\{\begin{array}{l}\bf y=\dfrac{x^2}{3}\\\bf \dfrac{x^4}{9}=3x\end{array}\right\ \ \ \bf \Rightarrow \ \ \ x^4=27x\ \ ,\ \ x\, (x^3-27)=0\ \ ,\\\\\\x_1=0\ \ ,\ \ x^3=27\ \ ,\ \ x_2=3$

а) Найдём площадь области как разность площадей криволинейных трапеций .

$\bf x^2=3y\ \ \Rightarrow \ \ \ y=\dfrac{x^2}{3}\ \ ;\ \ \ \ \ \ \ y^2=3x\ \ \Rightarrow \ \ \ y=\pm \sqrt{3x}$

$\displaystyle \bf S=\int\limits_0^3\, \sqrt{3x}\, dx-\int\limits_0^3\frac{x^2}{3}\, dx=\frac{\sqrt3\cdot \, x^{3/2}}{3/2}\, \Big|_0^3-\dfrac{x^3}{3\cdot 3}\Big|_0^3=\dfrac{2}{\sqrt3}\cdot \sqrt{x^3}\, \Big|_0^3-\frac{x^3}{9}\, \Big|_0^3=\\\\\\=\frac{2}{\sqrt3}\cdot \sqrt{27}-\frac{27}{9}=\frac{2}{\sqrt3}\cdot 3\sqrt3-3=6-3=3$

б) Объём тела, образованного вращением заданной фигуры вокруг оси OХ . Cчитаем как разность объёмов .

Формула объёма тела, образованного вращением криволинейной трапеции вокруг оси ОХ :

$\bf \displaystyle V_{ox}=\pi \int\limits_{a}^{b}\, y^2(x)\, dx$

$\displaystyle \bf V_{ox}=\pi \int\limits_0^3\, 3x\, dx-\pi \int\limits_0^3\, \frac{x^4}{9}\, dx=\pi \cdot \frac{3x^2}{2}\, \Big|_0^3-\pi \cdot \frac{x^5}{9\cdot 5}\, \Big|_0^3=\\\\\\=\pi \cdot \frac{3\cdot 9}{2}-\pi \cdot \frac{3^5}{3^2\cdot 5}=\pi \cdot \frac{27}{2}-\pi \cdot \frac{27}{5}=27\pi \cdot \Big(\frac{1}{2}-\frac{1}{5}\Big) =27\pi \cdot \frac{3}{10}=8,1\pi$

Приложения:

spamgg002: в моем профиле есть задачи на 100 баллов решите пожалуйста очень нужно

Автор ответа: FaerVator

Ответ:

а) S = 3(eд²)

b) V = 81π/10(eд³)

Пошаговое объяснение:

Сперво представим функции в удобном виде:

$1)x {}^{2} = 3y \\\\ y = \frac{x {}^{2} }{3} \\\\ y = \frac{1}{3} x {}^{2} \\\\ 2)y {}^{2} = 3x \\\\ y = \sqrt{3x}$

Понятно , что 1 график это то что синим цветом.

Найдём точки пересечения графиков этих функций:

$\displaystyle \sqrt{3x} = \frac{x^2}{3} \\\\ \left (3 \sqrt{3x} \right ) ^2 = \left ( x^2 \right )^2 \\\\ 27x -x^4 =0 \\\\ x\left (27-x^3 \right ) =0 \\\\ x_1=0~~~~~~~~~~~27-x^3=0;x^3=27 \Rightarrow x_2=3$

а)

Площадь фигуры ограниченной графиками функций вычисляется по формуле Ньютона - Лейбница:

$\boxed{ \boldsymbol{S = \int^b_af(x) dx= F(b) -F(a) \bigg |^b_a}}$

Где a и b - пределы интегрирования.

В нашем случае графики пересекаются в точке 0 и 3 - это пределы интегрирования . Так как на промежутке от 0 до 3 график 2-ой функции расположен выше , то от него нужно отнять график первой функции.

Находим площадь фигуры:

$S = \displaystyle \int^3_0\bigg ( \sqrt{3x} - \frac{1}{3} x {}^{2} \bigg ) dx = \displaystyle \int^3_0\bigg ( (3x) {}^{ \frac{1}{2} } - \frac{1}{3} x {}^{2} \bigg ) dx =\\\\= \frac{3 {}^{ \frac{3}{2} } \cdot 2x {}^{ \frac{3}{2} } }{ 3 } - \frac{x {}^{3} }{9} = \frac{2x \sqrt{3x} }{3} - \frac{x {}^{3} }{9} \bigg |^3_0 = \frac{6 \sqrt{9} }{3} - \frac{27}{9} - \bigg(0 - 0 \bigg ) = 6- 3 = 3\left ( ed^2\right )$

Объем тела полученная при вращения вокруг оси Ох вычисляется по формуле:

$\boxed{ \boldsymbol{V= \pi \int^b_af {}^{2} (x) dx}}$

Для того , чтобы найти объем тела, ограниченного графиками двух функций, нужно будет от объёма тела ограниченная графиком функции сверху(то есть это красный график) отнять объем тела , ограниченная графиком функции снизу( это синий график).

Пусть $V_2$ - объем тела, ограниченная функцией сверху , а $V_1$ - объем тела ограниченная функцией снизу.

Находим $V_2$ :

$\displaystyle V_2= \pi \int^3_0 \left ( \sqrt{3x} \right ) {}^{2} dx = \frac{ \pi \cdot3x {}^{2} }{2} \bigg |^3_0 = \frac{27 \pi}{2}$

Находим $V_1$ :

$\displaystyle V_1= \pi \int ^ 3_0\left ( \frac{x {}^{2} }{3} \right ) ^{2} dx = \pi\cdot \frac{1}{9} \int^3_0x^4dx=\frac{\pi \cdot x^5}{45} \bigg |^3_0=\frac{\pi \cdot 3^5}{45} =\frac{27\pi}{5}$