Предмет: Математика, автор: Змейкп

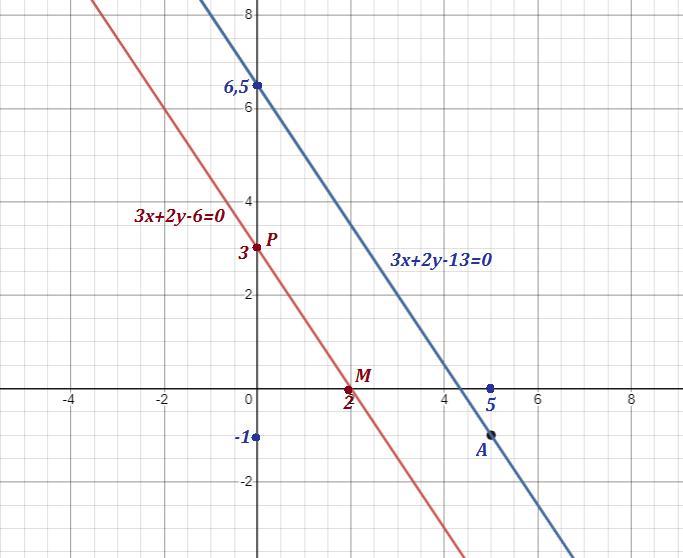
Найти уравнение прямой, проходящей через точку A(5; -1) параллельно прямой, отсекающей на положительных полуосях OX и OY отрезки равные 2 и 3 соответсвенно

Ответы

Автор ответа: NNNLLL54

0

Ответ:

Уравнение прямой, проходящей через точки М(2;0) и Р(0;3) ,

"в отрезках" имеет вид

$\bf \dfrac{x}{2}+\dfrac{y}{3}=1\ \ \ \Rightarrow \ \ \ 3x+2y=6\ \ ,\ \ 3x+2y-6=0$

Нормальный вектор этой прямой - это вектор $\bf \overline{n}=(\, 3\, ;\, 2\, )$ .

Так как искомая прямая параллельна заданной прямой, то их нормальные векторы коллинеарны . Искомая прямая проходит через точку А( 5;-1 ) . Её уравнение имеет вид

$\bf 3(x-5)+2(y+1)=0\ \ \Rightarrow \ \ \ 3x+2y-13=0$

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Українська література, автор: Sonechka2020

У новелі «Три зозулі з поклоном» НЕМАЄ такої композиційної особливості

Виберіть одну відповідь:
наявність обрамлення (розпитування сина матері) і трьох частин
повторюваний образ сосни
кульмінація на початку твору
зміщення часових площин

1 год назад

Предмет: Геометрия, автор: Mark007003

Знайдіть координати середини відрізка МН якщо м(-3;0;4), н(3;5;-2) ((багато балів!!!))) не пишіть будь ласка що не знаєте!

1 год назад

Предмет: Українська література, автор: Sonechka2020

В уривку …рокоче запорозька кров… наявний художній засіб

Виберіть одну відповідь:
символ
оксиморон
алітерація
метонімія

1 год назад

Предмет: Алгебра, автор: armyblackswan95

Помогите решить неравенство пожалуйста

7 лет назад

Предмет: Алгебра, автор: null000

Даю все баллы за решение:
Решите систему неравенств
{2х-3 <0
4х+7 >0

7 лет назад