Предмет: Алгебра, автор: Tvinkef

Помогите пожалуйста. Кому не лень.

Приложения:

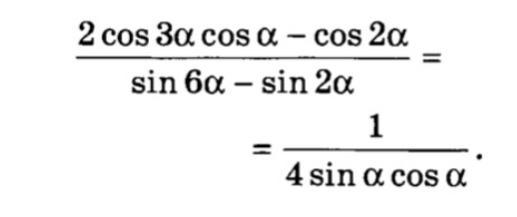
Ответы

Автор ответа: dinamungatova878

5

Ответ:

tga=sina/cosa.

cosa·sina/cosa+sina= 2sina.

2)(2sina+3cosa)^2= 4sin^2a+12sinacosa+9 cos^2a.

( 2cos альфа-3 sin альфа)^2= 4cos^2a-12cosasina+9sin^2a.

4sin^2a+12sinacosa+9 cos^2a+4cos^2a-12cosasina+9sin^2a=4(sin^2a+cos^2a)+9(sin^2a+cod^2a)=4+9=13.

12sinacosa- 12cosasina=0.

Объяснение:

Извините если не правильно.

Автор ответа: KOtikwe

1

Ответ:

Объяснение:

$\frac{2cos3\alphacos\alpha -cos2\alpha }{sin6\alpha -sin2\alpha } =\frac{1}{4sin\alpha cos\alpha }$

$\frac{2cos3\alpha cos\alpha -cos2\alpha }{2cos4\alpha sin2\alpha } =\frac{1}{2sin2\alpha }$

$\frac{2cos3\alpha cos\alpha -2cos2\alpha }{cos4\alpha } =1\\$

$8cos^4\alpha -6cos^2\alpha -cos^2\alpha +sin^2\alpha -cos^22\alpha +sin^22\alpha =0\\8cos^4\alpha -7cos^2\alpha -(cos^2\alpha -sin^2\alpha )^2+sin^22\alpha =0\\8cos^4\alpha -7cos^2\alpha -cos^4\alpha -sin^4\alpha +2sin^2\alpha cos^2\alpha +sin^22\alpha =0\\$

$7cos^4\alpha -7cos^2\alpha -sin^4\alpha +2sin^2\alpha cos^2\alpha +4sin^2\alpha cos^2\alpha =0\\7cos^2\alpha (cos^2\alpha -1)-sin^4\alpha +6sin^2\alpha cos^2\alpha =0\\-7cos^2\alpha +6sin^2\alpha cos^2\alpha -sin^4\alpha =0\\-sin^2\alpha cos^2\alpha -sin^4\alpha =0\\-sin^2\alpha (cos^2\alpha +sin^2\alpha )=0\\-sin^2\alpha =0\\x=k\pi$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: nadiakolomiec2012

Автомобіль рухався 3 год зі швидкістю 71,2 км/год і 2 год зі швидкістю 68,4 км/год. Знайдіть середню швидкість руху автомобіля. тільки не виразом !!!!!!!!!

1 год назад

Предмет: Математика, автор: dima702578

Нск 48 214. ПОМОГИТЕ ЕСЛИ ОТВЕТИТЕ 5 звёзд

1 год назад

Предмет: Психология, автор: deliseeva809

Проанализируйте особенности самооценки школьника с такими характеристиками: «Вова активен, стремится к достижению успеха как в учении, общественной работе, так и в играх. В любой деятельности он старается максимально самостоятельным, уверен в том, что можно добиться успеха собственными усилиями, не проявляет тревожности. Его можно назвать оптимистом».

1 год назад

Предмет: Математика, автор: lizasalomatina391

В книжном интернет-магазине было 3 000 экземпляров на-
учной фантастики на этой неделе в понедельник продали
530 книг, во вторник - 120. В среду - в 2 раза больше, чем
во вторник в четверг - на 100 книг меньше, чем в понедель-
ник. В пятницу - столько, сколько за период с понедельника
по четверг. В выходные - еще 100 книг. Остались ли ещё экземпляры научной фантастики в магазине и сколько?срочно!

7 лет назад

Предмет: Русский язык, автор: arinabolotniaia

Выполни Напиши эссе о природных чудесах, которые происходят в жизни Вселенной. (70 слов).Пожалуйста помогите

7 лет назад