Предмет: Геометрия,
автор: mosinalenni
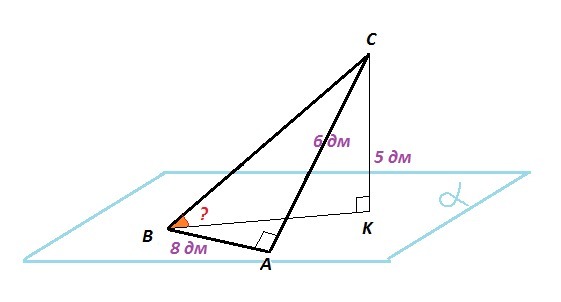
Через катет AB прямоугольного треугольника ABC проведена плоскость α. Найти угол наклона гипотенузы к плоскости α, если AC = 6 дм., AB = 8 дм, а точка C удалена от плоскости α на 5 дм.
Ответы
Автор ответа:
0
Дано: ΔABC - прямоугольный, ∠A = 90°, АС=6 дм, AB=8 дм;
AB ∈ α; CK ⊥ α; CK = 5 дм
Найти: ∠CBK - ?
Решение :
ΔABC : теорема Пифагора
BC² = AB² + AC² = 8² + 6² = 100 = 10²
BC = 10 дм
Угол наклона гипотенузы BC к плоскости α равен углу между гипотенузой BC и её проекцией BK на плоскость α.
ΔBCK - прямоугольный, ∠K = 90°.
Катет CK = 5 дм равен половине гипотенузы BC = 10 дм ⇒ катет CK лежит напротив угла 30° ⇒ ∠CBK = 30°
Ответ: 30°
Приложения:
Интересные вопросы
Предмет: Математика,
автор: Аноним
Предмет: Немецкий язык,
автор: svyatoslavagafonov20
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Геометрия,
автор: HellyWelly550