Предмет: Математика,
автор: melekhesenova736
6. Найти площадь пятиугольника ABCDE, если BD||AE, СК | АЕ , BD=10 см, AE=6 см, СК=12 см и ОК=8 см.
Приложения:
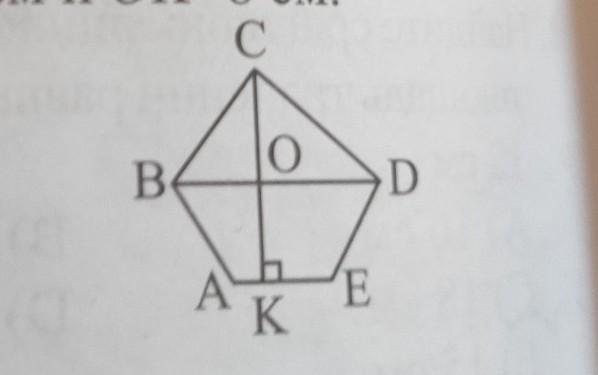
Ответы
Автор ответа:
0
Відповідь:
72 см²
Покрокове пояснення:
Площу п'ятикутника знайдемо як суму площ трикутника BCD та чотирикутника ABDE.
1) Так як BD║AE, CK ⊥ AE, то CO ⊥ BD, означає CO - висота трикутника BCD . Тоді площу трикутника BCD знайдемо за формулою:
S = *a*h
S = ·BD·CO =
·10·8= 80/2= 40 см²
2) Чотирикутник ABDE - трапеція, так як за умовою BD║AE
Тоді, S = ·( BD + AE)·OK
OK - висота трапеції і дорівнює СК - СО
ОК = СК-СО
ОК = 12 - 8 = 4 см
Отже, S = ·( 10 + 6)·4 =
*16*4 = 64/2=32 см²
3) Площа пятикутника: S = 40+ 32= 72 см²
Интересные вопросы
Предмет: Алгебра,
автор: goldilocks113
Предмет: Геометрия,
автор: TYuvelir
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: alenamuradanc4272
Предмет: География,
автор: fdsvoe