Предмет: Математика,
автор: yana2953
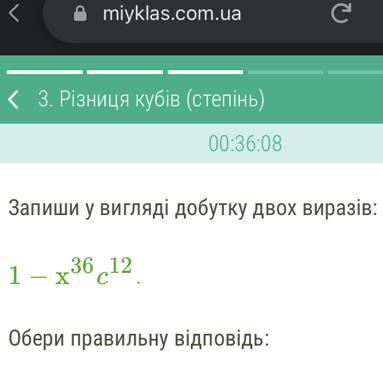
Срочно! Даю 40 балов! ПЖПЖПЖПЖПЖ
Приложения:
Ответы
Автор ответа:
0
Ответ:
Применяем формулу разности квадратов и
формулы суммы и разности кубов .
Интересные вопросы