Предмет: Алгебра, автор: Cap1918

Допоможіть терміново! Вища математика. Дослідити на абсолютну і умовну збіжність числові ряди. Детально на прикріпленому фото.
- Потрібне покрокове рішення. В кінці написати результат: збіжний чи розбіжний в залежності від результату. На папері, або зрозумілим шрифтом.
- Спам, або комменти не по темі = бан.

Приложения:

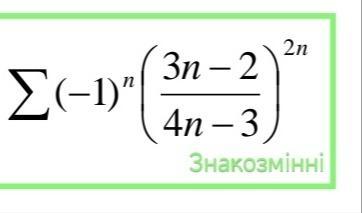
Ответы

Автор ответа: sangers1959

Пояснення:

$\displaystyle\\\sum\limits_{n=1}^\infty(-1)^n(\frac{3n-2}{4n-3} )^{2n}.$

Щоб дослідити цей ряд на збіжність/розбіжність треба перевірити

умови виконнання радикального правила Коші:

$\displaystyle\\\sum\limits_{n=1}^\infty |(-1)^n(\frac{3n-2}{4n-3} )^{2n})|=\sum\limits_{n=1}^\infty (\frac{3n-2}{4n-3} )^{2n}= \lim\limits_{n \to \infty} \sqrt[n]{(\frac{3n-2}{4n-3})^{2n} } =\\\\\\=\lim\limits_{n \to \infty}(\frac{3n-2}{4n-3})^{\frac{2n}{n} } } =\lim\limits_{n \to \infty}(\frac{3n-2}{4n-3})^2=\lim\limits_{n \to \infty}(\frac{n*(3-\frac{2}{n} )}{n*(4-\frac{3}{n}) } )^2=\\\\\\$

$\displaystyle\\=\lim\limits_{n \to \infty}(\frac{3-\frac{2}{n} }{4-\frac{3}{n} } )^2=(\frac{3-0}{4-0})^2 =(\frac{3}{4})^2=\frac{9}{16} < 1.\ \ \ \ \ \ \Rightarrow\\$