пж Постройте график функции f(x) = -2x² - х + 7 и, используя график, найдите: 1) вершину параболы и ось симметрии; 2) наибольшее значение и множество значений функции; 3) промежутки возрастания и убывания функции.
подробно и можно на фото
описывайте каждый пункт
спасибо заранее ​​

Решение.  

Графиком функции    является парабола .

Она проходит через точки    .

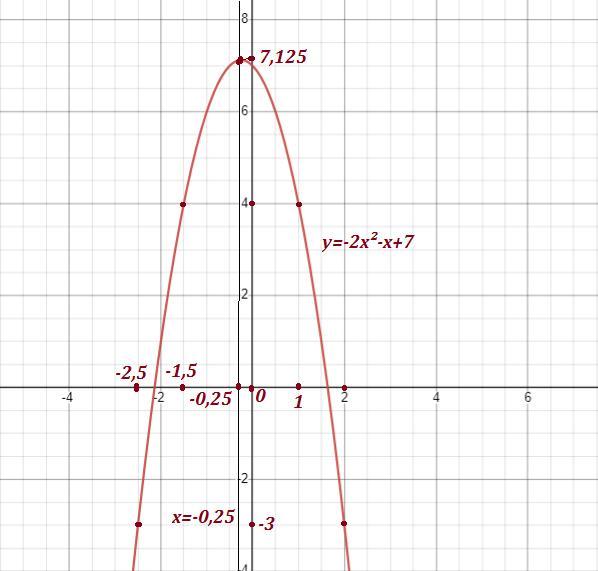
1)  Вершина параболы находится в точке  (-0,25 ; 7,125 ) , так как

Ось симметрии имеет уравнение  х = -0,25 .

2)  Наибольшее значение функция достигает в вершине при

х = -0,25 . Это значение равно  у(наибол.) = 7,125  .

3)  Промежуток возрастания :    .

Промежуток убывания :    .