Предмет: Алгебра, автор: veronikamila65

Помогите с решением пожалуйста

Приложения:

Ответы

Автор ответа: NNNLLL54

Ответ:

$\bf z=2x^2-5y^2$

Определение: линией уровня функции называется линия на плоскости , в каждой точке которой функция сохраняет постоянное значение .

Линиями уровня для данной функции будут линии, заданные

уравнением $\bf 2x^2-5y^2=C\ ,\ \ C=const$ .

$\bf C=0\ ,\ \ 2x^2-5y^2=0\ \ ,\ \ 5y^2=2x^2\ \ ,\ \, y^2=\dfrac{2}{5}\, x^2\ \ ,\ \ y=\pm \sqrt{0,4}x$

Это две прямые , пересекающиеся в начале координат .

$\bf C=1\ \ ,\ \ 2x^2-5y^2=1\ \ ,\ \ \dfrac{x^2}{0,5}-\dfrac{y^2}{0,2}=1$ . Это гипербола с центром в

начале координат и $\bf a=\sqrt{0,5}\ ,\ b=\sqrt{0,2}$ .

$\bf C=2\ ,\ \ 2x^2-5y^2=2\ \ ,\ \ \dfrac{x^2}{1}-\dfrac{y^2}{0,4}=1$ . Это гипербола с центром в

начале координат и $\bf a=1\ ,\ b=\sqrt{0,4}$ .

$\bf C=-1\ \ ,\ \ 2x^2-5y^2=-1\ \ ,\ \ -\dfrac{x^2}{0,5}+\dfrac{y^2}{0,2}=1$ . Это гипербола с

центром в начале координат и $\bf a=\sqrt{0,5}\ ,\ b=\sqrt{0,2}$ .

$\bf C=-2\ ,\ \ 2x^2-5y^2=-2\ \ ,\ \ -\dfrac{x^2}{1}+\dfrac{y^2}{0,4}=1$ . Это гипербола с

центром в начале координат и $\bf a=1\ ,\ b=\sqrt{0,4}$ .

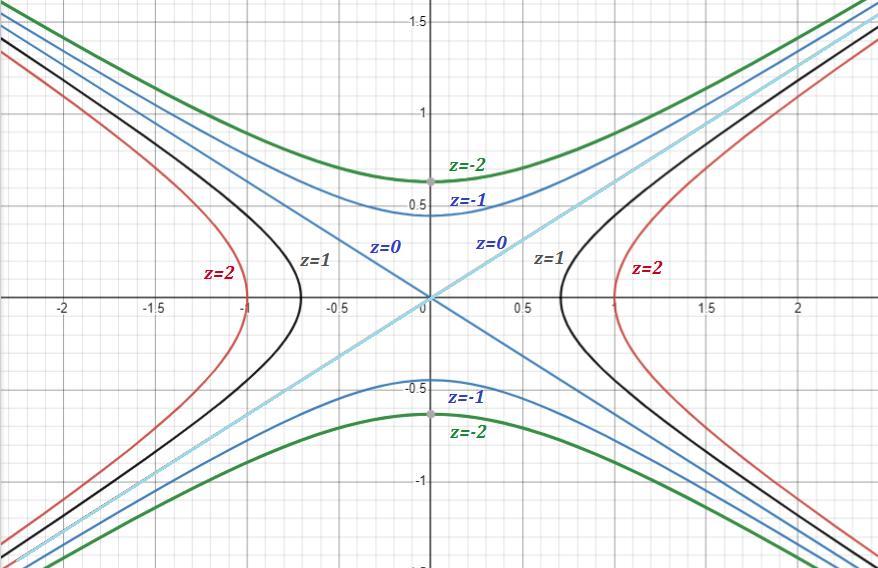
При C>0 линиями уровня являются гиперболы, ветви которых

симметричны оси абсцисс. При С<0 линиями уровня являются

гиперболы, ветви которых симметричны оси ординат . При С=0

линиями уровня являются две прямые, проходящие через начало

координат .

Приложения:

veronikamila65: спасибо большое

veronikamila65: я очень рада )

veronikamila65: осталось 1 вопрос, если сможете помогите и на этот вопрос пожалуйста, буду очень благодарна

NNNLLL54: там два одинаковых вопроса

veronikamila65: а ой не заметила , я добавила вопрос , там z=x^2-y^2.....

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Биология, автор: darinasupr

Яка роль людини у проведенні заходів щодо запобігання небезпечним природним явищам та їх наслідкам?

1 год назад

Предмет: Математика, автор: papasmpara

помогите пожалуста умоляю вас

1 год назад

Предмет: Английский язык, автор: onisenkom038

помогоите вставить нужные слова в текст

Do you think Yuppies is the name of extremely popular youth (C) all over

the world? The answer is ‘no’.

The __1__ ‘yuppie’ is basically an invention of the mass media, yuppies do

indeed exist. On the one hand, yuppies are the result of the__2__ against the

antiestablishment, against the free-minded 1960s’ __3__. But on the other

hand they are a phenomenon much more complex, tied to the nation’s economy.

What is a yuppie? A young urban professional, making a __4__ in busi-

ness. Being a yuppie is a __5__ of life. Those who want to be yuppies choose

the yuppie __6__ system. They conform __7__ the society standards. They

believe that money cures all illnesses. Yuppies are young: in their late twen-

ties or thirties. They are urban and often disapprove __8__ suburban life

style. Most of all, yuppies are professionals: they work __9__, rise quickly

and stop at nothing. They are more concerned __10__ enjoying their life

style than having a family or helping others in society.

1 год назад

Предмет: Английский язык, автор: pppp8ftKl

Раскройте скобки.
1.He (work) here since (come) to the city last year.
2.At 8 he (sit) in the library. He (read) some documents.
3.Mum I (make) pizza. Let’s eat it
4.I (paint) a new picture. Look at it.
5.They (consult) a doctor the other day.
6.I (eat ) my breakfast. Now I (go) to wash the dishes.
7.The lesson (finish) by 2 o’clock tomorrow.

7 лет назад

Предмет: Русский язык, автор: 6tatyana6

Запиши (заглавной буквой без точки в конце) букву, которой передан на письме чередующийся во втором слове согласный.

Тихий и тишина.
Простить и прощённый.

7 лет назад

Помогите с решением пожалуйста ​

Ответы

Помогите с решением пожалуйста