Предмет: Геометрия, автор: vitallativ211

Допоможіть будь ласочка я не розумію потрібно терміново. Зробіть з малюнком і дано. Точка простору знаходиться на відстані 10 см від кожної із сторін трикутника із сторонами 26 см, 26 см. 20 см. Знайти відстань від точки до площини трикутника.

Ответы

Автор ответа: ReMiDa

Ответ:

Відстань від точки до площини трикутника дорівнює

$\bf \dfrac{10\sqrt{5} }{3}$ см

Объяснение:

Точка простору знаходиться на відстані 10 см від кожної із сторін трикутника із сторонами 26 см, 26 см, 20 см. Знайти відстань від точки до площини трикутника.

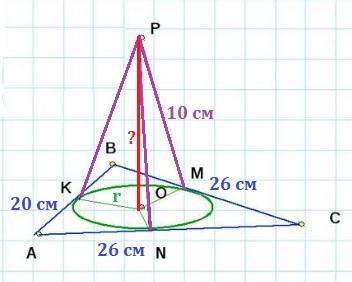
Опустимо з точки Р перпендикуляр РО до площини АВС. Проведемо перпендикуляри РК, РМ, РN до сторін АВ, ВС і АС відповідно.

За умовою РК=РМ=РN. Відрізки ОК, ОМ, ОN - проекції рівних похилих, тому ОК=ОМ=ОN.

За теоремою про три перпендикуляри ці проекції перпендикулярні до сторін ⇒ точка О рівновіддалена від сторін трикутника, тобто є центром вписаного у трикутник кола.

Якщо точка поза площиною трикутника рівновіддалена від усіх його сторін, то основою перпендикуляра, проведеного з даної точки до площини многокутника, є центр кола, вписаного в трикутник.

Для знаходження радіуса вписаного кола можна використати формулу:

$\bf r=\dfrac{S}{p}$

де S - площа трикутника, р - його півпериметр.

Площу трикутника легко обчислити за формулою Герона:

$\bf S=\sqrt{p(p-a)(p-b)(p-c)}$

Враховуючи, що а=26 см, b=26 см, с=20 см, маємо:

$\sf p=\dfrac{a+b+c}{2} =\dfrac{26+26+20}{2} =\bf 36$ (см)

Тому:

$\sf S=\sqrt{36(36-26)(36-26)(36-20)} =\sqrt{36*10*10*16} =\bf 240$ (см²)

$\sf r=\dfrac{240}{36} =\bf \dfrac{20}{3}$ (см)

Розглянемо прямокутний ΔКРО (∠О=90°) , у якого гипотенуза КР=10 см, катет КО=20/3 см. За теоремою Пифагора знайдемо катет РО:

$\sf PO=\sqrt{KP^{2}-KO^{2} } =\sqrt{10^{2} -{(\frac{20}{3} )}^{2} } =\\\\=\sqrt{100-\frac{400}{9} } =\sqrt{\frac{900-400}{9} } =\sqrt{\frac{500}{9} } =\bf \dfrac{10\sqrt{5} }{3}$ (см)