Предмет: Алгебра, автор: masha01021

найдите экстремум функции
Помогите пожалуйста решить

Приложения:

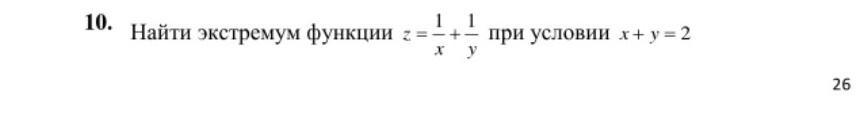
Ответы

Автор ответа: NNNLLL54

Ответ:

Найти условный экстремум функции $\bf z=\dfrac{1}{x}+\dfrac{1}{y}$ при условии $\bf x+y=2$

Сначала нужно представить уравнение связи в виде $\bf \varphi (x;y)=0$ и

составить функцию Лагранжа : $\bf L=f(x;y)+\lambda \cdot \varphi (x;y)$ .

$\bf \varphi (x;y)=x+y-2=0$

$\bf L=\dfrac{1}{x}+\dfrac{1}{y}+\lambda \cdot (x+y-2)$

Найдём частные производные функции Лагранжа, при этом с $\bf \lambda$ следует обращаться, как с константой .

$\bf L'_{x}=-\dfrac{1}{x^2}+\lambda \ \ ,\ \ L'_{y}=-\dfrac{1}{y^2}+\lambda$

Составим и решим следующую систему:

$\left\{\begin{array}{l}\bf L'_{x}=0\\\bf L'_{y}=0\\\bf \varphi (x;y)=0\end{array}\right\ \ \left\{\begin{array}{l}\bf -\dfrac{1}{x^2}+\lambda =0\\\bf -\dfrac{1}{y^2}+\lambda =0\\\bf x+y-2=0\end{array}\right\ \ \left\{\begin{array}{l}\bf \lambda =\dfrac{1}{x^2}\\\ \bf \lambda =\dfrac{1}{y^2}\\\bf x+y-2=0\end{array}\right\ \ \left\{\begin{array}{l}\bf \dfrac{1}{x^2}=\dfrac{1}{y^2}\\\bf x+y-2=0\end{array}\right$

$\left\{\begin{array}{l}\bf y^2=x^2\\\bf x+y-2=0\end{array}\right\ \ \left\{\begin{array}{l}\bf y=\pm x\\\bf x+y-2=0\end{array}\right\ \ \left\{\begin{array}{l}\bf y_1=x\ ,\ y_2=-x\\\bf x+y-2=0\end{array}\right$

$\bf a)\ \ \left\{\begin{array}{l}\bf y_1=x\\\bf x+x-2=0\end{array}\right\ \ \left\{\begin{array}{l}\bf y_1=x\\\bf 2x-2=0\end{array}\right\ \ \left\{\begin{array}{l}\bf y=1\\\bf x=1\end{array}\right \ \ ,\ \ \lambda =1\\\\\\b)\ \ \left\{\begin{array}{l}\bf y_2=-x\\\bf x-x-2=0\end{array}\right\ \ \left\{\begin{array}{l}\bf y_2=-x\\\bf 0-2=0\end{array}\right\ \ \ \Rightarrow \ \ net\ reshenij$

Подставим в уравнение связи найденные значения переменных .

$\bf x+y-2=0\ \ \Rightarrow \ \ \ x+x-2=0\ \ ,\ \ 2x-2=0\ \ ,\ \ x=1\\\\1+y-2=0\ \ \Rightarrow \ \ y=1$

Получили одну стационарную точку $\bf M_0(\, 1\, ;\, 1\, )$ .

Проверим выполнение достаточного условия экстремума для найденной стационарной точки.

Способ основан на использовании дифференциала второго порядка $\bf d^2L$ .

$\bf d^2L=L''_{xx}(dx)^2+2\, L''_{xy}+L''_{yy}(dy)^2\\\\L''_{xx}=\Big(-\dfrac{1}{x^2}+\lambda \Big)'_{x}=-(-2)\cdot x^{-3}=\dfrac{2}{x^3}\ \ ,\ \ \ \ \ L''_{yy}=\dfrac{2}{y^3}\ \ ,\\\\L''_{xy}=\Big(-\dfrac{1}{x^2}+\lambda \Big)'_{y}=0$