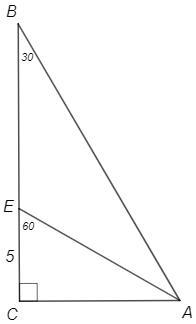
3. В прямоугольном треугольнике ABC 2C=90° и 2B-30°. На отрезке ВС взята точка Е таким образом, что AEC=60°. Найдите длину стороны ВЕ, если ЕС=5 см.​

Рассмотрим треугольник с углами 30°, 60°, 90°

Катет против угла 30 равен половине гипотенузы.

Пусть этот катет x, гипотенуза 2x

Второй катет по теореме Пифагора =√(4x^2 -x^2) =x√3

Доказали, что в треугольнике с углами 30°, 60°, 90° стороны относятся 1 : √3 : 2

CE/AC =1/√3

AC/BC =1/√3

=> CE/BC =1/3

=> CE/BE =1/2 => BE=10 (см)