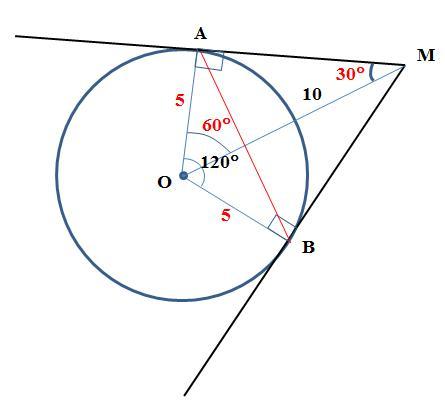
из точки М к окружности с центром О проведены касательные МА и МВ. найдите расстояние между точками касания А и В, если угол АОВ = 120 градусам и МО = 10

Ответ:

Объяснение:

Нужно знать:

1. Радиус окружности, проведенный в точку касания, перпендикулярен касательной.

2. Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

3. В прямоугольном треугольнике напротив угла в 30 градусов лежит катет, равный половине гипотенузы.

4. Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними.

Решение. Так как радиусы OA и OB окружности перпендикулярны (свойство 1) касательным MA и MB, соответственно, то образуются равные (два катета одного треугольника равны двум катетам другого) прямоугольники OAM и OBM: OA = OB - радиусы, (свойство 2) MA=MB - отрезки касательных (см. рисунок).

По условию ∠AOB = 120°, значит ∠AOM=60° и ∠AMO=30°. Тогда, в силу свойства 3, OM = 10 и радиусы OA=OB=10:2=5.

Теперь применим теорему косинусов:

SPJ1