Решите, пожалуйста, правую часть (98, 100, 102 , 104). Хотя бы 1 или 2 номера.

Объяснение:

98.

диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам:

АО=ОС=16:2=8

ВО=ОD=BD:2=18:2=9

∆BOC - прямоугольный:

по теореме Пифагора:

ВС=√(ВО²+ОС²)=√(9²+8²)=√145

∆МВС - прямоугольный:

по теореме Пифагора:

МВ=√(МС²-ВС²)=√(17²-(√145)²)=√144=12

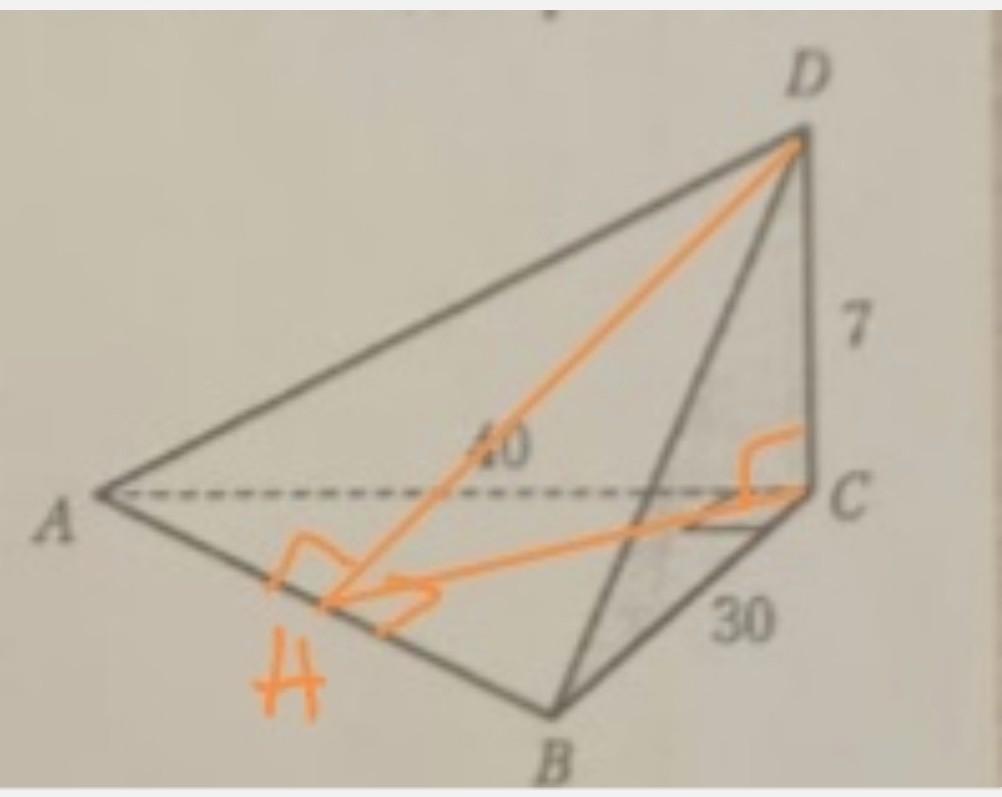
100.

если DC⟂(ABC),то DC⟂CH.

CH является проекцией DH

по теореме о трёх перпендикулярах

СН⟂АВ => DH⟂AB

DH=?

S(ABC)=1/2•AC•BC=1/2•40•30=600

S(ABC)=1/2•AB•CH

CH=2S(ABC)/AB

по теореме Пифагора:

AB=√(АС²+ВС²)=√(40²+30²)=√2500=50

СН=2•600/50=24

∆DHC -прямоугольный:

по теореме Пифагора:

DH=√(DC²+CH²)=√(7²+24²)=√625=25

102.

ABCD - квадрат ,тогда

АВ=BC=CD=AD=√36=6

∆АМВ - прямоугольный:

по теореме Пифагора:

АМ=√(МВ²+АВ²)=√(8²+6²)=√100=10

АВ⟂АD,то по теореме о трёх перпендикуляр ах МА⟂АD

∆MAD -прямоугольный:

S(AMD)=1/2•AD•AM=1/2•6•10=30

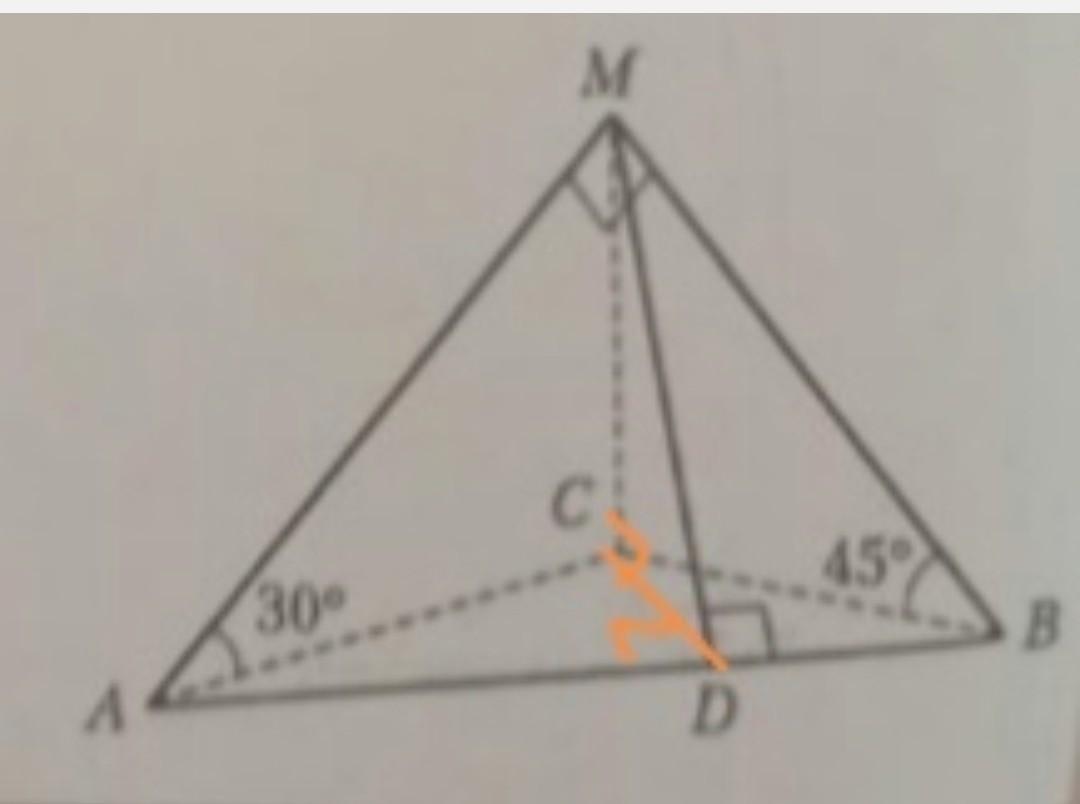
104.

по теореме о трёх перпендикулярах:

СD⟂AB=>MD⟂AB.

∠MDC=?

∆MCB - прямоугольный:

sin∠СВМ=MC/MB =>MB=МС/sin45=

=MC/(√2/2)=2MC/√2=√2MC

∆AMC - прямоугольный:

Катет лежащий против угла 30° равен половине гипотенузы:

АМ=2•МС

∆АМВ - прямоугольный:

по теореме Пифагора:

АВ=√(АМ²+МВ²)=

=√((2МС)²+(√2МС)²)=

=√(4МС²+2МС²)=МС√6

S(ABM)=1/2•AB•MD

S(ABM)=1/2•AM•MB

1/2•AB•MD=1/2•AM•MB

AB•MD=AM•MB

MC√6•MD=2MC•√2MC

MD=2√2MC²/√6MC=2MC/√3

sin∠MDC=MC/MD=

=MC/(2MC/√3)=√3/2

∠MDC=60°