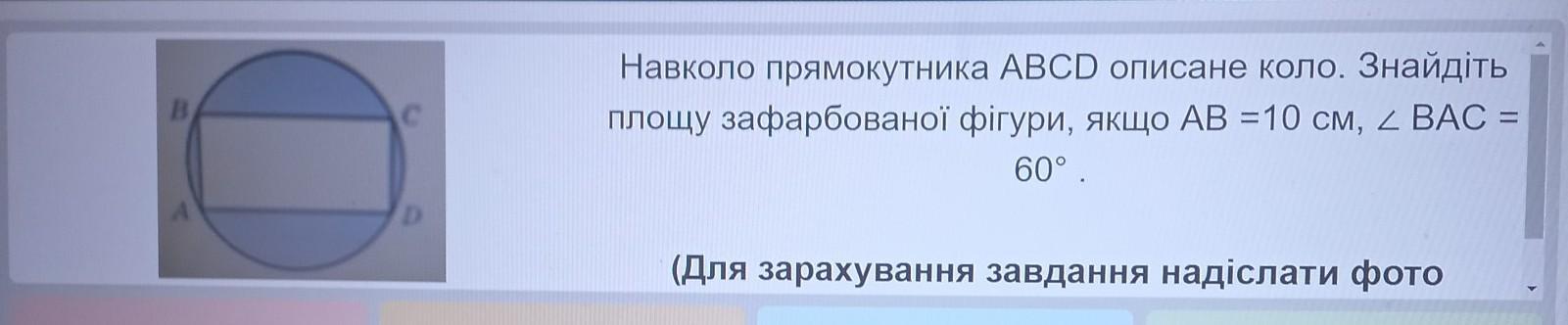
Навколо прямокутника ABCD описане коло. Знайдіть площу зафарбованоï фігури, якщо AB =10 см, < BAC = 60°. (Для зарахування завдання надіслати фото​

Ответ:

Спочатку знайдемо радіус описаного кола навколо прямокутника ABCD. Він дорівнює половині діагоналі прямокутника:

r = AC/2 = AB√3/2 = 5√3 см.

Тепер розділим зафарбовану фігуру на дві частини - трикутник ABO та сектор кола AOCB. Щоб знайти площу трикутника, знайдемо його висоту OH, яка є серединним перпендикуляром до сторони AB:

OH = AB/2 = 5 см.

Тоді площа трикутника ABO дорівнює:

S_triangle = 1/2 * AB * OH = 1/2 * 10 * 5 = 25 см^2.

Щоб знайти площу сектора, спочатку знайдемо його центральний кут за формулою:

α = 360° - 2 * < BAC = 240°

Тоді площа сектора дорівнює:

S_sector = α/360° * πr^2 = 240°/360° * π * (5√3)^2 = 25π см^2.

Отже, загальна площа зафарбованої фігури дорівнює:

S = S_triangle + S_sector = 25 + 25π ≈ 97,4 см^2.

Объяснение: