Предмет: Математика, автор: hihidic623

Похідна та ее застосування тема пж срочно нужно

Приложения:

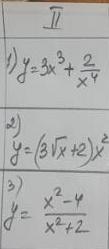
Ответы

Автор ответа: natalyabryukhova

Ответ:

1) $\displaystyle y'=9x^2-\frac{8}{x^5}$

2) $\displaystyle y'=7\frac{1}{2}x\sqrt{x} +4x$

3) $\displaystyle y'=\frac{12x}{(x^2+2)^2}$

Пошаговое объяснение:

Найти производную.

Надо знать формулы:

$\displaystyle \bf (x^n)' =nx^{n-1}\\\\(uv)'=u'v+uv'\\\\\left(\frac{u}{v}\right)'=\frac{u'v-uv'}{v^2}$

1) $\displaystyle \bf y=3x^3+\frac{2}{x^4}=3x^3+2x^{-4}$

$\displaystyle y'=3\cdot3x^2+2\cdot (-4)\vdot x^{-4-1}=9x^2-8x^{-5}=9x^2-\frac{8}{x^5}$

2) $\displaystyle \bf y=(3\sqrt{x} +2)\cdot x^2=(3x^{\frac{1}{2} }+2)\cdot x^2$

$\displaystyle y'=3\cdot\frac{1}{2} x^{-\frac{1}{2} }\cdot x^2+(3x^{\frac{1}{2} }+2)\cdot 2x=\\\\=\frac{3x^2}{2\sqrt{x} } +6x\sqrt{x} +4x=\frac{3}{2}x\sqrt{x} +6x\sqrt{x} +4x=\\ \\=7\frac{1}{2}x\sqrt{x} +4x$

3) $\displaystyle \bf y=\frac{x^2-4}{x^2+2}$

$\displaystyle y'=\frac{2x\cdot(x^2+2)-(x^2-4)\cdot2x}{(x^2+2)^2} =\\\\=\frac{2x(x^2+2-x^2+4)}{(x^2+2)^2} =\frac{12x}{(x^2+2)^2}$

lybkivskyiyra: Помогите мне пожалуйста Наталья

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Физика, автор: zensusk

Какой импульс он передал столу, если шарик массой 100 грамм упал на поверхность стола с высоты 40 см и был перенесен на высоту 30 см?

дано:
m=100кг=0,1кг
h1=40см=0,4м
h2=30см=0,3м
p=?

формула:
h=h1+h2
v=√2gh
p=mv

решение:
h=0,4м+0,3м=0,7м
v=√2×10м/с²×0,7м=3,8м/с

так я дал решение и мне нужно что-то связанное с импульсом надо проверить этой формулой
m1×v1→+m2v2→=m2v1→`+m2v2→`

надо написать два раза проверить
если что → наверху v а " ` " так называемый штрих вроде , короче те кто шарят за физику помогите пожалуйста .

1 год назад

Предмет: Русский язык, автор: juliatolstaja

углу́бите и углуби́те разобрать по составу оба слова

1 год назад

Предмет: Русский язык, автор: eghiazaryansyuzi007

Подберите синонимы к словам преподаватель, школьники, школа, ребята, превосходный, чистая (правда), ничуть (не бывало), убирали (лестницу ветками), огромная (цифра), не врал, нетрудно.

1 год назад

Предмет: Геометрия, автор: liliyakovalchuk15

периметр ромба дорівнює 40 см а його менша діагональ 12 см знайти площу ромба
Нада срочно!!!!!

7 лет назад

Предмет: Русский язык, автор: aidarvashenok

Определите часть речи каждого слова

7 лет назад