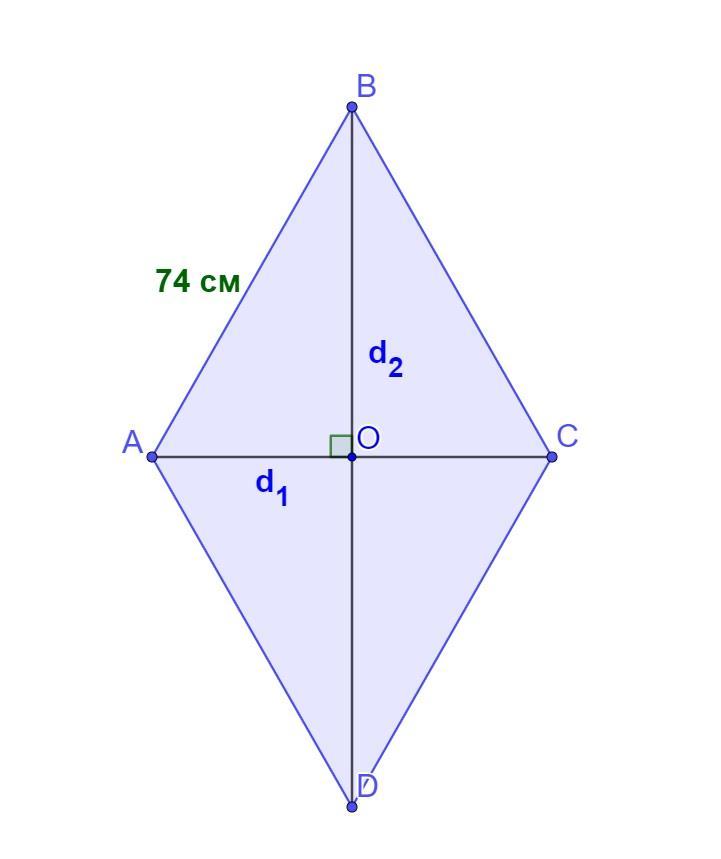
3. Знайти площу ромба, якщо його діагоналi вiдносяться як 12 : 35, а сторона дорівнює 74 см.​

Ответ:

Площа ромба ддорівнює 3360 см²

Объяснение:

Знайти площу ромба, якщо його діагоналi вiдносяться як 12 : 35, а сторона дорівнює 74 см.

Дано: ABCD - ромб, АВ=74 см, d₁ : d₂ = 12 : 35

Знайти: S

Розв'язання:

Площу ромба знайдемо за формулою:

Нехай d₁ = 12х, d₂= 35х, де х-коефіцієнт пропорційності.

Відомо, що діагоналі ромба перпендикулярні між собою та перехрещуються в його центрі, тому розглянемо прямокутний трикутник АОВ (∠АОВ=90°).

Так як діагоналі ромба точкою перетину діляться навпіл,то:

Гіпотенуза АВ=74 см

За теоремою Піфагора маємо:

144x²+1225x²=21904

1369x²=21904

x²=16

x₁=-4 (не задовольняє умові)

х₂=4

Отже, d₁ = 12·4=48 (см), d₂= 35·4=140 (см)

 (cм²)

Відповідь: 3360 см²

#SPJ1