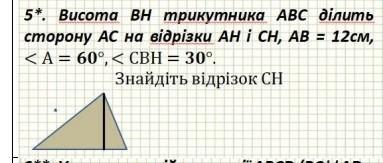
Висота BH трикутника АВС ділить
сторону АС на вiдрiзки АН i CH, AB = 12cm,
<A = 60º < CBH = 30º
= 60°
Знайдіть відрізок CH​

Ответ:

З огляду на те, що BH є висотою трикутника ABC, ми можемо скористатися теоремою синусів, щоб знайти відрізок CH.

Згідно з теоремою синусів, відношення довжини сторони трикутника до синуса протилежного кута є для всіх сторін співмірним:

AC / sin(A) = AB / sin(B) = BC / sin(C)

Ми знаємо довжину сторони AB, а також кути A і CBH, тому ми можемо використати це відношення, щоб знайти довжину сторони BC:

BC / sin(60°) = 12 / sin(30°)

BC = 12 * sin(60°) / sin(30°)

BC = 24 cm

Тепер, ми можемо використати те саме відношення, щоб знайти довжину відрізка CH:

CH / sin(CBH) = BC / sin(A)

CH / sin(30°) = 24 / sin(60°)

CH = 24 * sin(30°) / sin(60°)

CH = 12 cm

Отже, довжина відрізка CH дорівнює 12 см.