решите пожалуйста
ДАЮ 25 БАЛЛОВ
Ответы
Ответ:
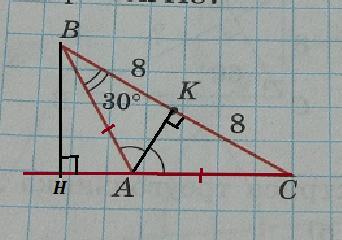
Дан ΔАВС , ∠АВК=30° , ∠ВАК=∠САК , ВК=СК=8 .
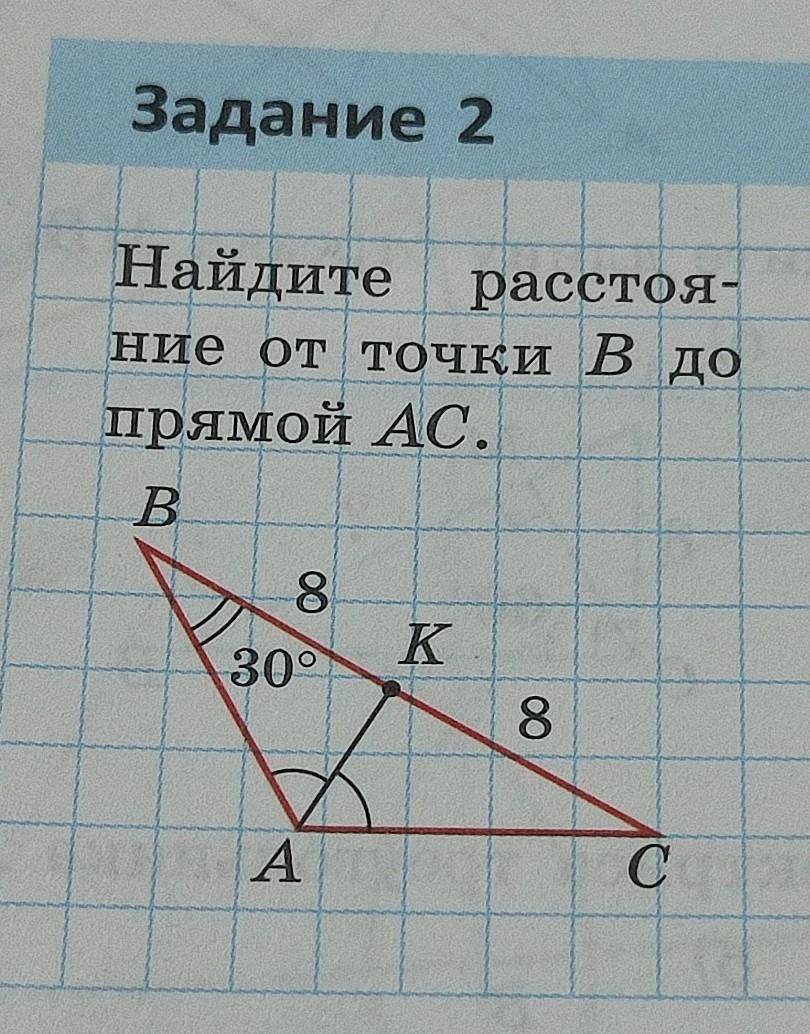
Найти расстояние от т. В до прямой АС .
Расстояние от т. В до прямой АС равно длине перпендикуляра, опущенного из т. В на сторону треугольника АС , то есть высоте АН треугольника АВС , АН ⊥ АС .
Так как ∠ВАК=∠САК и ВК=СК , то АК - биссектриса и медиана ΔАВС , значит ΔАВС- равнобедренный , AB=AC , и к тому же АК ещё и высота, проведённая из вершины А на основание ВС .
Поэтому ΔАВК- прямоугольный , ∠АКВ=90° .
В этом треугольнике катет АК, лежащий против угла в 30° равен половине гипотенузы АВ , то есть если обозначить АВ=а , то АК=а/2 .
По теореме Пифагора АВ²=АК²+ВК² ⇒ а²=(а²/4)+8² , 3а²/4=64 ,
а²=(64 · 4)/3 ⇒ а=(8 · 2)/√3 = 16/√3 ⇒ а/2 = 8/√3 .
P.S. Можно было найти АВ и ВК , используя тригонометрические функции , если уже учили их . tg∠B=AK/BK ⇒ tg30°=AK/8 ,
AK=8·tg30°=8·(1/√3)=8/√3 ⇒ AB=AK/sin30°=(8/√3)/(1/2)=16/√3
Так как АС=АВ=16/√3 , то площадь ΔАВС равна S=1/2 · AC · AH .
S=1/2 · (16/√3) ·AH = (8/√3) ·AH
Но площадь ΔАВС можно вычислить по другому : S=1/2 · BC · AK ,
S=1/2 ·(8+8) · (8/√3) = 64/√3
Приравняем выражения для площади ΔАВС .
(8/√3) ·AH =64/√3 ⇒ AH=(64/√3) : (8/√3) = 64/8=8
Ответ: AH=8 .