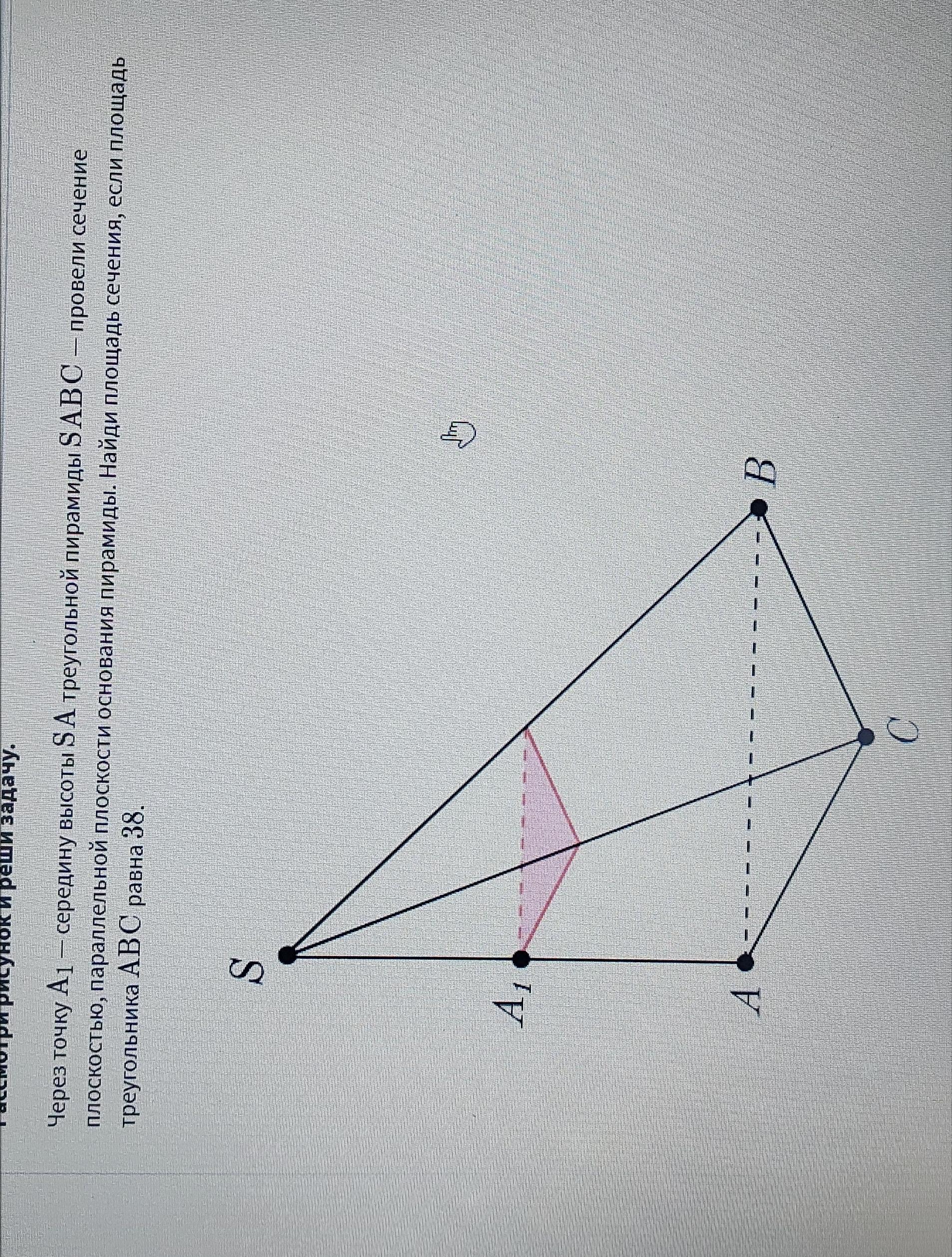
через точку а1 середину высоты sa треугольной пирамиды sabc провели сечение плоскостью параллельной плоскости основания пирамиды. найди площадь сечения если площадь треугольника abc равна 38

Ответ:

Пошаговое объяснение:

Для начала найдем высоту пирамиды.

Очевидно, что треугольник sa1c подобен треугольнику abc, так как эти треугольники имеют два равных угла (угол a1sc соответствует углу asc, а угол с точкой a1 — это прямой угол, который соответствует углу с основанием). Значит, отношение соответствующих сторон равно отношению высот треугольников:

sa1/sa = a1c/ac

sa1/sa = 1/2  (так как точка a1 — это середина высоты sa)

Отсюда получаем:

sa1 = sa/2

Таким образом, высота s находится на расстоянии h = sa/2 от точки a1 (так как точка а1 — это середина высоты sa).

Теперь рассмотрим плоскость, проходящую через точку а1 и параллельную основанию. Пересечение этой плоскости с боковой гранью sabc даст нам треугольник a1bcd.

Этот треугольник подобен треугольнику abc, так как у них две пары соответственных углов (углы a1 и bcd — прямые, а углы abc и acd равны в силу параллельности плоскостей основания и сечения). Отношение соответствующих сторон равно отношению высот треугольников:

a1b/ab = a1c/ac = a1d/ad = h/sa

Отсюда получаем:

a1b = ab × h/sa

a1d = ad × h/sa

Так как точка а1 является серединой высоты sabc из вершины s, то можно заметить, что треугольник a1sd подобен треугольнику abc. Значит, отношение соответствующих сторон равно отношению высот:

a1s/as = a1d/ad = h/sa

Отсюда получаем:

a1s = as × h/sa

Теперь можно выразить площадь треугольника a1bcd через площадь треугольника abc:

S(a1bcd) = S(abc) × (a1b/ab) × (a1d/ad)

S(a1bcd) = 38 × (ab × h/sa)/ab × (ad × h/sa)/ad

S(a1bcd) = 19 × h^2/sa^2 × ab × ad

Так как sa^2 = ab^2 − (ab/2)^2 (теорема Пифагора для треугольника sab), то

S(a1bcd) = 19 × h^2 × ab × ad/(4(ab^2 − ab^2/4))

S(a1bcd) = 76 × h^2/3ab

Осталось выразить высоту h через площадь:

ab = 2S(abc)/sa (так как sa = 2S(abc)/ab)

h = 2S(sabc)/(sa × ab) = (sa/2) × 2S(abc)/(sa × ab) = (S(abc)/ab)

Теперь можем выразить площадь сечения через площадь треугольника abc:

S(сечения) = S(a1bcd) + S(a1sd)

S(сечения) = 76 × h^2/3ab + a1s × a1d/2

S(сечения) = 76 × (S(abc)/ab)^2/3ab + as × ad × h^2/sa^2 × 1/2

S(сечения) = 38 × (S(abc))^2/sa^2ab + as × ad × S(abc)/sa^2

Так как ab = 2S(abc)/sa, то

S(сечения) = 38 × (S(abc))^2/sa^3 + 2S(abc) × S(abc)/sa^3

S(сечения) = 40 × S(abc)/sa^2

Подставляя значение S(abc) = 38, получим:

S(сечения) = 40/4

S(сечения) = 10

Таким образом, площадь сечения равна 10.