Предмет: Алгебра, автор: natwqq2

8 класс , алгебра
$.$

Приложения:

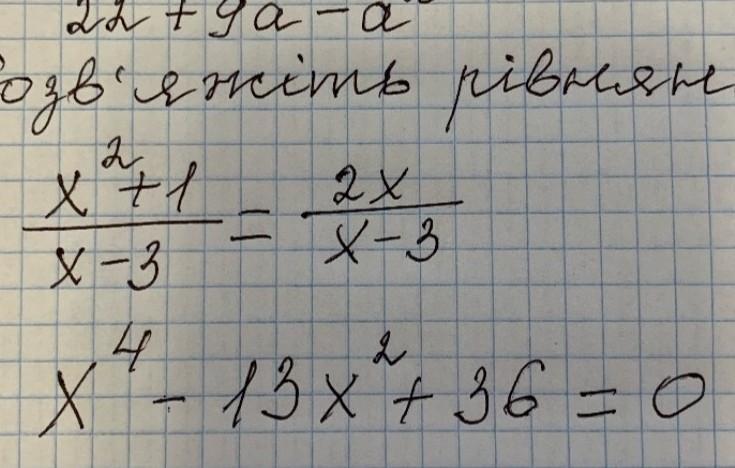
Ответы

Автор ответа: mathkot

1

Ответ:

Решения уравнений:

1) $\boldsymbol{\boxed{x=1}}$

2) $\boldsymbol{\boxed{ x_{1,2} = \pm 3; x_{3,4} = \pm 2}}$

Объяснение:

1)

$\dfrac{x^{2} +1}{x-3} = \dfrac{2x}{x-3}$

ОДЗ: $x \in \mathbb R \backslash \{3\}$

$\dfrac{x^{2} +1}{x-3} = \dfrac{2x}{x-3} \bigg | \cdot (x- 3)$

$x^{2} +1 = 2x$

$x^{2} - 2x + 1 = 0$

$(x - 1)^{2} = 0 \Longleftrightarrow x - 1 = 0 \Longrightarrow x = 1$

2)

$x^{4} - 13x^{2} + 36 = 0$

Замена: $x^{2} = t; t \geq 0$

$t^{2} - 13t + 36 = 0$

$D = 169 - 4 \cdot 1 \cdot 36 = 169 - 144 = 25 = 5^{2}$

$t_{1} = \dfrac{13+ 5}{2} = \dfrac{18}{2} = 9$

$t_{2} = \dfrac{13 - 5}{2} = \dfrac{8}{2} = 4$

$\left[ \begin{gathered} x^{2} = t_{1} \\ x^{2} =t_{2} \\ \end{gathered} \right.$ $\left[ \begin{gathered} x^{2} =9 \\ x^{2} =4 \\ \end{gathered} \right.$ $\left[ \begin{gathered} \sqrt{x^{2} } =\sqrt{9} \\ \sqrt{x^{2} } =\sqrt{4} \\ \end{gathered} \right.$ $\left[ \begin{gathered} |x| =3 \\ |x| =2 \\ \end{gathered} \right.$ $\left[ \begin{gathered} x_{1,2} = \pm 3 \\ x_{3,4} = \pm 2 \\ \end{gathered} \right.$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Алгебра, автор: Gsjqwsooq

Знайти значення виразу
3х⁶у², якщо 3х³у=-6

1 год назад

Предмет: Українська мова, автор: saburlaka2810

Складіть і запишіть діалог-обмін думками з приводу збереження пам'яток історії та культури (по 6 реплік з кожної сторони)
Срочно!!!

1 год назад

Предмет: Литература, автор: oooqjejejejehhdh

5. Вирішивши зіграти роль зрадника, який шлях порятунку для монголів запропонував Максим? СРОЧНОООО ДАЮ 20 БАЛЛОВ

1 год назад

Предмет: Алгебра, автор: andreyhi

помогите пожалуйста:-(

7 лет назад

Предмет: Геометрия, автор: vladsabar2017

5 - 9 классы Геометрия 5+3 б
Градусна міра гострого кута прямокутного трикутника дорівнює 38º. Знайдіть градусну міру іншого гострого кута цього трикутника.
А)52º
Б) 26º
В) 73º
Г) 90º
СРОЧНО КР ПИШУ!!!!!

7 лет назад