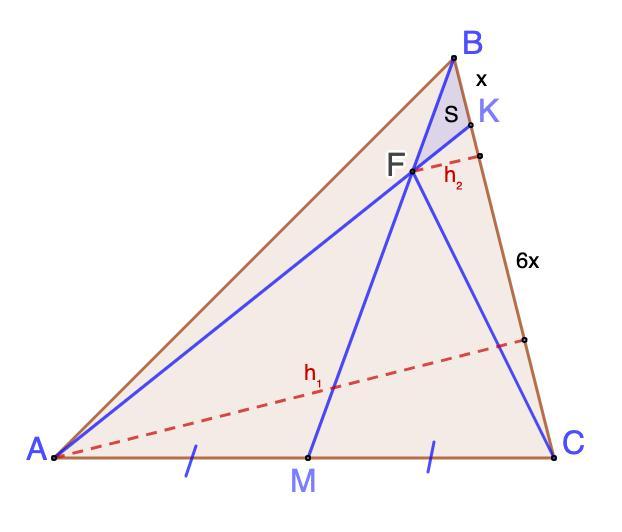
Предмет: Геометрия, автор: sonya7132

Площа трикутника ABC дорівнює 56 см^2. На стороні BC
позначили точку K так, що BK:KC=1:6. Відрізок AK перетинає медіану BM у точці F. Знайдіть площу трикутника CKF.

Ответы

Автор ответа: natalyabryukhova

Ответ:

Площадь треугольника CKF равна 6 см².

Объяснение:

Площадь треугольника ABC равна 56 см². На стороне BC обозначили точку K так, что BK : KC = 1 : 6. Отрезок AK пересекает медиану BM в точке F. Найдите площадь треугольника CKF.

Дано: ΔАВС;

S(ABC) = 56 см²;

К ∈ ВС; BK : KC = 1 : 6;

BM - медиана; AK ∩ BM = F.

Найти: S(CKF)

Решение:

1. Рассмотрим ΔАВС.

ВМ - медиана.

Медиана треугольника делит его на два равновеликих треугольника.

⇒ S(ABM) = S(MBC)

2. Рассмотрим ΔAFC.

FM - медиана.

⇒ S(AFM) = S(MFC)

3. Рассмотрим ΔABF и ΔFBC

S(ABF) = S(ABM) - SAFM)

S(FBC) = S(MBC) - S(MFC)

⇒ S(ABF) = S(FBC)

4. BK : KC = 1 : 6

Пусть ВК = х см, тогда КС = 6х см, а ВС = 7х см.

5. Рассмотрим ΔАВК и ΔАВС.

Они имеют одинаковую высоту h₁.

Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.

$\displaystyle \frac{S(ABK)}{S(ABC)}=\frac{BK}{BC} =\frac{x}{7x}\\ \\ \frac{S(ABK)}{56} =\frac{1}{7}\;\;\;\Rightarrow \;\;\;S(ABK)=\frac{56}{7}=8\;_{(CM^2)}$