Точка О — центр вневписанной окружности треугольника АВС, касающейся его стороны АС. Найдите угол АОС, если угол АВС равен 50°.

Ответ:

∠AOC =90 -B/2 =90-25 =65°

Объяснение:

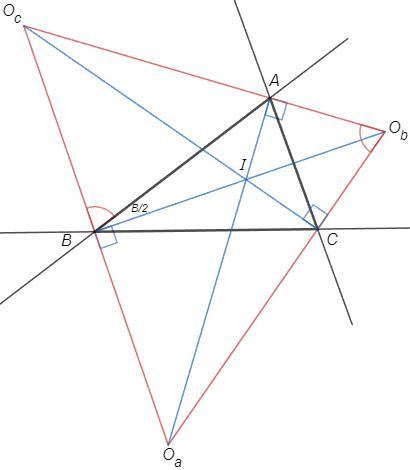
Центр вневписанной окружности - пересечение внешних и внутренней биссектрис.

Внешняя и внутренняя биссектрисы при одной вершине перпендикулярны.

Отрезок OaOb виден из точек A и B под прямым углом, следовательно точки A-B-Oa-Ob на окружности.

Тогда =180

Или

I - инцентр

A/2 +B/2 +C/2 =90 => ∠AIC=90 +B/2

Cумма противоположных углов AOCI равна 180

=> ∠AOC=90 -B/2